题目内容
已知P={x|1≤x≤9，x∈N}，记f（a，b，c，d）=ab-cd，（其中a，b，c，d∈P），例如：f（1，2，3，4）=1×2-3×4=-10．设u，v，x，y∈P，且满足f（u，v，x，y）=39和f（u，y，x，v）=66，则有序数组（u，v，x，y）是______．
由已知f（u，v，x，y）=39和f（u，y，x，v）=66，得
两式作差可得（u+x）（y-v）=27
∵27=3×9
∴u+x=9，y-v=3，代入数验证得（u，v，x，y）=（8，6，1，9）
故应填（8，6，1，9）．
|
∵27=3×9
∴u+x=9，y-v=3，代入数验证得（u，v，x，y）=（8，6，1，9）
故应填（8，6，1，9）．
练习册系列答案
阅读快车系列答案
相关题目
，
，且
，
（t为参数）．在极坐标系（与直角坐标系xoy取相同的长度单位，且以原点O为极点，以x轴正半轴为极轴）中，圆C的方程为
．
，
，
，且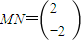
，
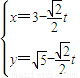（t为参数）．在极坐标系（与直角坐标系xoy取相同的长度单位，且以原点O为极点，以x轴正半轴为极轴）中，圆C的方程为
．
，