题目内容
已知P={x|1≤x≤9，x∈N}，记f（a，b，c，d）=ab-cd，（其中a，b，c，d∈P），例如：f（1，2，3，4）=1×2-3×4=-10．设u，v，x，y∈P，且满足f（u，v，x，y）=39和f（u，y，x，v）=66，则有序数组（u，v，x，y）是分析：根据运算规则将题设中的关系转化为方程组，再据方程组进行判断求解，本题判断时要把数据代入题设中的两个条件以及推理出的条件进行综合判断．
解答：解：由已知f（u，v，x，y）=39和f（u，y，x，v）=66，得
两式作差可得（u+x）（y-v）=27
∵27=3×9
∴u+x=9，y-v=3，代入数验证得（u，v，x，y）=（8，6，1，9）
故应填（8，6，1，9）．
|
∵27=3×9
∴u+x=9，y-v=3，代入数验证得（u，v，x，y）=（8，6，1，9）
故应填（8，6，1，9）．
点评：本题考点是算法，根据新定义规则进行运算，求得参数的值，代入验证时不要漏条件．
练习册系列答案
相关题目
，
，且
，
（t为参数）．在极坐标系（与直角坐标系xoy取相同的长度单位，且以原点O为极点，以x轴正半轴为极轴）中，圆C的方程为
．
，
，
，且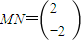
，
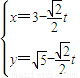（t为参数）．在极坐标系（与直角坐标系xoy取相同的长度单位，且以原点O为极点，以x轴正半轴为极轴）中，圆C的方程为
．
，