题目内容
周长为2的直角三角形的面积的最大值为
3-2
| 2 |
3-2
.| 2 |
分析:设直角三角形的两直角边为a、b,斜边为c,因为L=a+b+c,c=
,两次运用均值不等式即可求解.
| a2+b2 |
解答:解:设直角三角形的两直角边分别为a、b,斜边为c,则直角三角形的面积S=
ab.
由已知,得a+b+c=2,∴a+b+
=2,
∴2=a+b+
≥2
+
=(2+
)
,
∴
≤
=2-
,∴ab≤(2-
)2=6-4
,
∴S=
ab≤3-2
,当且仅当a=b=2-
时,S取最大值3-2
.
故答案为:3-2
.
| 1 |
| 2 |
由已知,得a+b+c=2,∴a+b+
| a2+b2 |
∴2=a+b+
| a2+b2 |
| ab |
| 2ab |
| 2 |
| ab |
∴
| ab |
| 2 | ||
2+
|
| 2 |
| 2 |
| 2 |
∴S=
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
故答案为:3-2
| 2 |
点评:利用均值不等式解决实际问题时,列出有关量的函数关系式或方程式是均值不等式求解或转化的关键.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
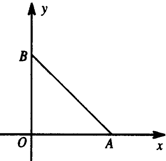 在如图所示的平面直角坐标系中,三角形AOB是腰长为2的等腰直角三角形,动点P与点O位于直线AB的两侧,且∠APB=
在如图所示的平面直角坐标系中,三角形AOB是腰长为2的等腰直角三角形,动点P与点O位于直线AB的两侧,且∠APB= B.
B. C.
C. D.
D.