Question

如图，在△ABC中，已知顶点B(9,1),C(3,4)和内心I(4,1)，求顶点A的坐标.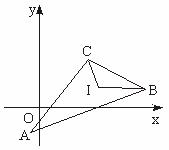

Answer 1

解法一：由B(9,1)和C(3,4)，得BC的方程为x＋2y－11=0.

点I(4,1)到BC的距离为=.

设AB、AC的方程分别为y－1=k_AB(x－9),y－4=k_AC(x－3),即k_ABx－y－9k_AB＋1=0,k_ACx－?y－3k_AC＋4=0.

又∵I为内心到各边距离相等，

∴=，=.

解得k_AB=±,k_AC=2或k_AC=－.

由图知AB、AC的倾斜角均为锐角，∴k_AB=,k_AC=2.

∴AB和AC的方程分别为x－2y－7=0和2x－y－2=0.

解方程组求得顶点A的坐标为(－1,－4).

解法二：∵BI∥x轴，∠CBI=∠ABI,

∴AB与BC关于BI对称，且直线BC的倾斜角与直线AB的倾斜角互补.

而k_BC==－,∴k_AB=.

∴AB的方程为y－1=(x－9),即x－2y－7=0.

又∵AC到IC的角等于IC到BC的角，且k_IC==－3，∴=.解得k_AC=2.∴AC的方程为y－4=2(x－3),即2x－y－2=0.

解方程组得顶点A(－1，－4).