题目内容
已知抛物线x2=4y的焦点为F，直线y=kx+1与抛物线交于A，B两点，过A，B两点分别作抛物线的切线，设其交点为M。
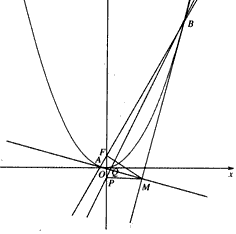
（1）当k=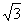
时，证明：FM⊥AB；
（2）若过点M作y轴的垂线，垂足为P，点A关于y轴的对称点为Q，求证：P，Q，B三点共线。
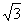时，证明：FM⊥AB；（2）若过点M作y轴的垂线，垂足为P，点A关于y轴的对称点为Q，求证：P，Q，B三点共线。
解：（1）F（0，1），设A（x1，y1），B（x2，y2），
将y= kx+1代入抛物线x2=4y得x2-4ky-4=0
∴当k=
时，
∵抛物线方程为x2=4y，即
∴过抛物线上A，B两点的切线方程分别是
∴两条切线的交点M的坐标为
∴
故FM⊥AB。
（2）由上可知
且 Q（-x1， y1），
P的坐标为
而
因为x2（y1+1） +x1（y2+1）=2kx1x2+2（x1+x2）=-8k+8k=0
所以
从而P，Q，B三点共线。
将y= kx+1代入抛物线x2=4y得x2-4ky-4=0
∴当k=
时，∵抛物线方程为x2=4y，即
∴过抛物线上A，B两点的切线方程分别是
∴两条切线的交点M的坐标为
∴
故FM⊥AB。
（2）由上可知
且 Q（-x1， y1），
P的坐标为
而
因为x2（y1+1） +x1（y2+1）=2kx1x2+2（x1+x2）=-8k+8k=0
所以
从而P，Q，B三点共线。
练习册系列答案
相关题目
已知抛物线x2=4y上的点P（非原点）处的切线与x轴，y轴分别交于Q，R两点，F为焦点．
（2009•温州一模）如图，已知抛物线x2=4y，过抛物线上一点A（x1，y1）（不同于顶点）作抛物线的切线l，并交x轴于点C，在直线y=-1上任取一点H，过H作HD垂直x轴于D，并交l于点E，过H作直线HF垂直直线l，并交x轴于点F．
（2011•浙江模拟）已知抛物线x2=4y，圆C：x2+（y-2）2=4，M（x0，y0），（x0＞0，y0＞0）为抛物线上的动点．