题目内容
已知函数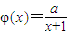 ,a为正常数.
,a为正常数.(1)若f(x)=lnx+φ(x),且
 ,求函数f(x)的单调增区间;
,求函数f(x)的单调增区间;(2)若g(x)=|lnx|+φ(x),且对任意x1,x2∈(0,2],x1≠x2,都有
 ,求a的取值范围.
,求a的取值范围.
【答案】分析:(1)先对函数y=f(x)进行求导,然后令导函数大于0(或小于0)求出x的范围,根据f′(x)>0求得的区间是单调增区间,f′(x)<0求得的区间是单调减区间,即可得到答案.
(2)设h(x)=g(x)+x,依题意得出h(x)在(0,2]上是减函数.下面对x分类讨论:①当1≤x≤2时,②当0<x<1时,利用导数研究函数的单调性从及最值,即可求得求a的取值范围.
解答:解:(1) ,(2分)
,(2分)
∵ ,令f′(x)>0,得x>2,或
,令f′(x)>0,得x>2,或 ,
,
∴函数f(x)的单调增区间为 ,(2,+∞).(6分)
,(2,+∞).(6分)
(2)∵ ,
,
∴ ,
,
∴ ,(8分)
,(8分)
设h(x)=g(x)+x,依题意,h(x)在(0,2]上是减函数.
当1≤x≤2时, ,
, ,
,
令h′(x)≤0,得: 对x∈[1,2]恒成立,
对x∈[1,2]恒成立,
设 ,则
,则 ,
,
∵1≤x≤2,∴ ,
,
∴m(x)在[1,2]上递增,则当x=2时,m(x)有最大值为 ,
,
∴ (12分)
(12分)
当0<x<1时, ,
, ,
,
令h′(x)≤0,得: ,
,
设 ,则
,则 ,
,
∴t(x)在(0,1)上是增函数,
∴t(x)<t(1)=0,
∴a≥0,(15分)综上所述, (16分)
(16分)
点评:本小题主要考查函数单调性的应用、利用导数研究函数的单调性、导数的几何意义、不等式的解法等基础知识,考查运算求解能力,属于基础题.
(2)设h(x)=g(x)+x,依题意得出h(x)在(0,2]上是减函数.下面对x分类讨论:①当1≤x≤2时,②当0<x<1时,利用导数研究函数的单调性从及最值,即可求得求a的取值范围.
解答:解:(1)
 ,(2分)
,(2分)∵
 ,令f′(x)>0,得x>2,或
,令f′(x)>0,得x>2,或 ,
,∴函数f(x)的单调增区间为
 ,(2,+∞).(6分)
,(2,+∞).(6分)(2)∵
 ,
,∴
 ,
,∴
 ,(8分)
,(8分)设h(x)=g(x)+x,依题意,h(x)在(0,2]上是减函数.
当1≤x≤2时,
 ,
, ,
,令h′(x)≤0,得:
 对x∈[1,2]恒成立,
对x∈[1,2]恒成立,设
 ,则
,则 ,
,∵1≤x≤2,∴
 ,
,∴m(x)在[1,2]上递增,则当x=2时,m(x)有最大值为
 ,
,∴
 (12分)
(12分)当0<x<1时,
 ,
, ,
,令h′(x)≤0,得:
 ,
,设
 ,则
,则 ,
,∴t(x)在(0,1)上是增函数,
∴t(x)<t(1)=0,
∴a≥0,(15分)综上所述,
 (16分)
(16分)点评:本小题主要考查函数单调性的应用、利用导数研究函数的单调性、导数的几何意义、不等式的解法等基础知识,考查运算求解能力,属于基础题.

练习册系列答案
相关题目
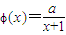 ,a为正常数.
,a为正常数. ,求函数f(x)的单调增区间;
,求函数f(x)的单调增区间;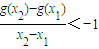 ,求a的取值范围.
,求a的取值范围.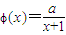 ,a为正常数.
,a为正常数. ,求函数f(x)的单调增区间;
,求函数f(x)的单调增区间;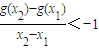 ,求a的取值范围.
,求a的取值范围.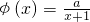 ,a为正常数.
,a为正常数.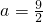 ,求函数f(x)的单调增区间;
,求函数f(x)的单调增区间;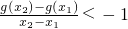 ,求a的取值范围.
,求a的取值范围.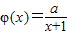 ,a为正常数.
,a为正常数.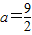 ,求函数f(x)的单调增区间;
,求函数f(x)的单调增区间;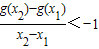 ,求a的取值范围.
,求a的取值范围.