题目内容
函数f(x)=xex-a有两个零点,则实数a的取值范围是________.
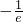 <a<0
<a<0分析:由函数的解析式,求出函数的导函数,由导数法,可得当x=-1时,函数取最小值,若函数有两个零点,则最小值f(-1)<0,结合a≥0时,x∈(-∞,-1)时,f(x)=xex-a<0恒成立,不存在零点,可得实数a的取值范围
解答:∵函数f(x)=xex-a的导函数f′(x)=(x+1)ex,
令f′(x)=0,则x=-1
∵当x∈(-∞,-1)时,f′(x)<0,函数f(x)单调递减;
当x∈(-1,+∞)时,f′(x)>0,函数f(x)单调递增;
故当x=-1时,函数取最小值f(-1)=-e-1-a
若函数f(x)=xex-a有两个零点,则f(-1)=-e-1-a<0
即a>
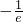
又∵a≥0时,x∈(-∞,-1)时,f(x)=xex-a<0恒成立,不存在零点
故a<0
综上,
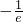 <a<0
<a<0故答案为:
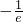 <a<0
<a<0点评:本题考查的知识点是根的存在性及根的个数判断,其中熟练掌握函数零点与方程根之间的对应关系是解答的关键,解答时易忽略a≥0时,x∈(-∞,-1)时,f(x)=xex-a<0恒成立,不存在零点,而错解为a>
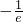 .
. 
练习册系列答案
相关题目
函数f(x)=-
(a<b<1),则( )
| x |
| ex |
| A、f(a)=f(b) |
| B、f(a)<f(b) |
| C、f(a)>f(b) |
| D、f(a),f(b)大小关系不能确定 |