题目内容
若函数f(x)=2sin(ωx+φ),对于任意x都有f(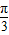 -x)=f(
-x)=f(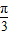 +x),则f(
+x),则f(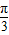 )等于( )
)等于( )A.0
B.2
C.
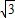
D.2或-2
【答案】分析:由y=f(x)满足f(a+x)=f(a-x),则y=f(x)图象关于x=a对称,函数f(x)在x=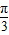 处取的最值,即得结论.
处取的最值,即得结论.
解答:解:由于如果函数y=f(x)满足f(a+x)=f(a-x),则y=f(x)图象关于x=a对称,
故x=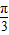 为函数f(x)=2sin(ωx+φ)的对称轴,
为函数f(x)=2sin(ωx+φ)的对称轴,
即函数f(x)=2sin(ωx+φ)在x=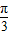 处取的最值±2,
处取的最值±2,
故答案为 D
点评:本题考查函数的图象与图象变化,求解的关键是熟练掌握函数的图象的变换规则以及一些常见函数的对称性如y=f(x)满足f(a+x)=f(a-x),则y=f(x)图象关于x=a对称,y=f(x)与f(-x)的图象关于x=0对称等.
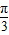 处取的最值,即得结论.
处取的最值,即得结论.解答:解:由于如果函数y=f(x)满足f(a+x)=f(a-x),则y=f(x)图象关于x=a对称,
故x=
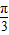 为函数f(x)=2sin(ωx+φ)的对称轴,
为函数f(x)=2sin(ωx+φ)的对称轴,即函数f(x)=2sin(ωx+φ)在x=
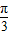 处取的最值±2,
处取的最值±2,故答案为 D
点评:本题考查函数的图象与图象变化,求解的关键是熟练掌握函数的图象的变换规则以及一些常见函数的对称性如y=f(x)满足f(a+x)=f(a-x),则y=f(x)图象关于x=a对称,y=f(x)与f(-x)的图象关于x=0对称等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
定义在R上的函数y=f(x)是减函数,且函数y=f(x-1)的图象关于(1,0)成中心对称,若s,t满足不等式f(s2-2s)≤-f(2t-t2).则当1≤s≤4时,
的取值范围是( )
| t |
| s |
A、[-
| ||
B、[-
| ||
C、[-
| ||
D、[-
|