题目内容
极坐标系的极点是直角坐标系的原点,极轴为x轴正半轴.已知曲线C1的极坐标方程为ρ=2cosθ,曲线C2的参数方程为
(其中t为参数,α为字母常数且α∈[0,π))
(1)求曲线C1的直角坐标方程和曲线C2的普通方程;
(2)当曲线C1和曲线C2没有公共点时,求α的取值范围.
|
(1)求曲线C1的直角坐标方程和曲线C2的普通方程;
(2)当曲线C1和曲线C2没有公共点时,求α的取值范围.
解析:(1)由ρ=2cosθ得ρ2=2ρcosθ
所以x2+y2=2x,即曲线C1:x2+y2-2x=0
曲线C2:(tanα)x-y+
-2tanα=0…(4分)
…(8分)
…(10分)
所以x2+y2=2x,即曲线C1:x2+y2-2x=0
曲线C2:(tanα)x-y+
| 3 |
|
…(10分)

练习册系列答案
相关题目
 选修4-4:坐标系与参数方程
选修4-4:坐标系与参数方程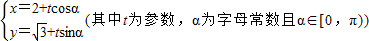
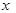 轴正半轴。已知曲线
轴正半轴。已知曲线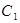 的极坐标方程为
的极坐标方程为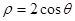 ,曲线
,曲线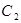 的参数方程为
的参数方程为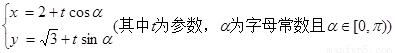
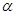 的取值范围。
的取值范围。 轴的正半轴重合.曲线
轴的正半轴重合.曲线 的极坐标方程为
的极坐标方程为 ,曲线
,曲线 的极坐标方程是
的极坐标方程是 .
.
 ,
, 两点,求
两点,求 .
.