题目内容
设f1(x)= ,fn+1(x)=f1[fn(x)],且an=
,fn+1(x)=f1[fn(x)],且an=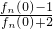 ,则a2011=________.
,则a2011=________.

分析:根据已知可得
 =
= =
= =
= ,结合等比数列的通项公式可求an,进而可求
,结合等比数列的通项公式可求an,进而可求解答:∵f1(0)=2,
 =
=
∴fn+1(0)=f1[fn(0)]=

∴
 =
= =
= =
=
∴数列{an}是首项为
 为首项,以
为首项,以 为公比的等比数列
为公比的等比数列∴

∴
 =
=
故答案为:

点评:本题以函数为载体,考查数列的通项,考查等比数列的定义,等比数列的通项公式的应用,具有一定的综合性

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
已知f(x)=
,设f1(x)=f(x),fn(x)=fn-1[fn-1(x)](n>1,n∈N*),则f3(x)和fn(x)的表达式分别为( )
| x |
| 1-x |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
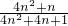 (n∈N*),试比较9T2n与Qn的大小,并说明理由.
(n∈N*),试比较9T2n与Qn的大小,并说明理由.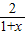 ,定义fn+1 (x)=f1[fn(x)],an=
,定义fn+1 (x)=f1[fn(x)],an= (n∈N*).
(n∈N*).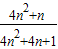 (n∈N*),试比较9T2n与Qn的大小,并说明理由.
(n∈N*),试比较9T2n与Qn的大小,并说明理由.