题目内容
1.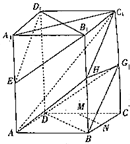 如图,在平行六面体ABCD-A1B1C1D1中,E,M,N,G分别是AA1,CD,CB,CC1的中点.
如图,在平行六面体ABCD-A1B1C1D1中,E,M,N,G分别是AA1,CD,CB,CC1的中点.(1)若平行六面体ABCD-A1B1C1D1为棱长是2的正方体,求四面体A1B1D1E的体积和表面积;
(2)求证;MN∥B1D1;
(3)求证:平面EB1D1∥∥平面BDG.
分析 (1)分别求出${S}_{△{A}_{1}{D}_{1}E}$,${S}_{△{A}_{1}{B}_{1}E}$,${S}_{△{A}_{1}{B}_{1}{D}_{1}}$,${S}_{△{B}_{1}{D}_{1}E}$,由此能求出四面体A1B1D1E的体积和表面积.
(2)由已知得BD∥MN,BD∥B1D1,由此能证明MN∥B1D1.
(3)由已知得BD∥B1D1,BG∥D1E,由此能证明平面EB1D1∥∥平面BDG.
解答 (1)解:∵平行六面体ABCD-A1B1C1D1为棱长是2的正方体,
∴${S}_{△{A}_{1}{D}_{1}E}$=${S}_{△{A}_{1}{B}_{1}E}$=$\frac{1}{2}×2×1$=1,
${S}_{△{A}_{1}{B}_{1}{D}_{1}}$=$\frac{1}{2}×2×2$=2,
${S}_{△{B}_{1}{D}_{1}E}$=$\frac{1}{2}×\sqrt{4+4}×\sqrt{1+2}$=$\sqrt{6}$,
∴四面体A1B1D1E的体积:
${V}_{E-{A}_{1}{B}_{1}{D}_{1}}$=$\frac{1}{3}×{A}_{1}E×{S}_{△{A}_{1}{B}_{1}{D}_{1}}$=$\frac{1}{3}×1×2$=$\frac{2}{3}$.
四面体A1B1D1E的表面积:
S=${S}_{△{A}_{1}{D}_{1}E}$+${S}_{△{A}_{1}{B}_{1}E}$+${S}_{△{A}_{1}{B}_{1}{D}_{1}}$+${S}_{△{B}_{1}{D}_{1}E}$=1+1+2+$\sqrt{6}$=4+$\sqrt{6}$.
(2)证明:∵在平行六面体ABCD-A1B1C1D1中,M,N,G分别是CD,CB,CC1的中点,
∴BD∥MN,BD∥B1D1,
∴MN∥B1D1.
(3)证明:∵在平行六面体ABCD-A1B1C1D1中,E,M,N,G分别是AA1,CD,CB,CC1的中点,
∴BD∥B1D1,BG∥D1E,
∵BD∩BG=B,B1D1∩D1E=D1,
∴平面EB1D1∥∥平面BDG.
点评 本题考查四面体的体积和表面积的求法,考查直线与直线平行的证明,考查面面平行的证明,是中档题,解题时要注意空间思维能力的培养.

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | sin2<sin3 | B. | cos2<cos3 | C. | tan2<tan3 | D. | cot2<cot3 |
| A. | 13 | B. | 14 | C. | 15 | D. | 16 |