题目内容
(本小题满分12分)
已知函数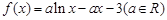 .
.
(I)当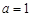 时,求函数
时,求函数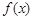 的单调区间;
的单调区间;
(II)若函数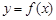 的图象在点
的图象在点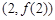 处的切线的倾斜角为45o,问:m在什么范围取值时,对于任意的
处的切线的倾斜角为45o,问:m在什么范围取值时,对于任意的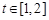 ,函数
,函数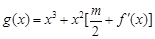 在区间
在区间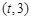 上总存在极值?
上总存在极值?
(1)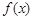 在(0,1)上单调递增,在(1,+∞)上单调递减.
在(0,1)上单调递增,在(1,+∞)上单调递减.
(2)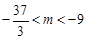 。
。
解析试题分析: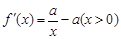
(I)当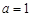 时,
时,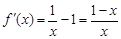 ,
,
令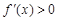 时,解得
时,解得 ,所以
,所以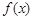 在(0,1)上单调递增;
在(0,1)上单调递增;
令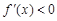 时,解得
时,解得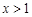 ,所以
,所以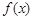 在(1,+∞)上单调递减.
在(1,+∞)上单调递减.
(II)因为函数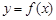 的图象在点(2,
的图象在点(2, )处的切线的倾斜角为45o,
)处的切线的倾斜角为45o,
所以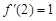 .
.
所以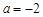 ,
,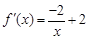 .
. 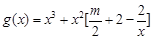
 ,
, ,
,
因为任意的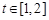 ,函数
,函数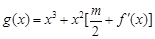 在区间
在区间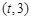 上总存在极值,
上总存在极值,
所以只需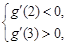
解得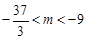 .
.
考点:利用导数研究函数的单调性和极值;导数的几何意义。
点评:(1)本题注意考查导数知识的运用,利用导数来研究函数的单调性很热极值,同时也考查了学生分析问题、解决问题的能力,属于中档题.(2)利用导数求函数的单调区间,一定要先求函数的定义域。(3)要满足函数y=f(x)在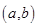 内有极值点。只需满足
内有极值点。只需满足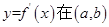 内有变号零点。
内有变号零点。

练习册系列答案
相关题目
 ,设AB=2x,BC=y.
,设AB=2x,BC=y.
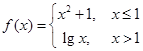 ,则
,则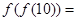 _______________.
_______________.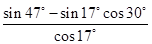 =____________.
=____________. (单位:千套)与销售价格
(单位:千套)与销售价格 (单位:元/套)满足的关系式
(单位:元/套)满足的关系式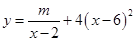 ,其中
,其中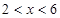 ,
,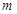 为常数.已知销售价格为4元/套时,每日可售出套题21千套.
为常数.已知销售价格为4元/套时,每日可售出套题21千套.
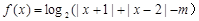 .
. 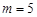 时,求函数
时,求函数 的定义域;
的定义域;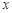 的不等式
的不等式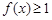 的解集是
的解集是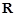 ,求
,求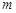 的取值范围.
的取值范围.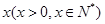 户农民从事蔬菜加工,则剩下的继续从事蔬菜种植的农民平均每户的年收入有望提高
户农民从事蔬菜加工,则剩下的继续从事蔬菜种植的农民平均每户的年收入有望提高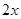 %,而从事蔬菜加工的农民平均每户的年收入将为
%,而从事蔬菜加工的农民平均每户的年收入将为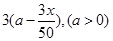 万元.
万元.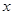 户农民从事蔬菜加工后,要使从事蔬菜种植的农民的总年收入不低于动员前从事蔬菜种植的农民的总年收入,求
户农民从事蔬菜加工后,要使从事蔬菜种植的农民的总年收入不低于动员前从事蔬菜种植的农民的总年收入,求 的最大值.
的最大值.