题目内容
各项均为正数的数列{an}中,设 ,
, ,且
,且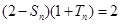 ,
, .
.
(1)设 ,证明数列{bn}是等比数列;
,证明数列{bn}是等比数列;
(2)设 ,求集合
,求集合 .
.
 ,
, ,且
,且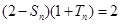 ,
, .
.(1)设
 ,证明数列{bn}是等比数列;
,证明数列{bn}是等比数列;(2)设
 ,求集合
,求集合 .
.(1)详见解析,(2)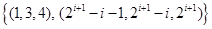 (
(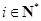 ).
).
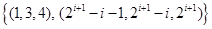 (
(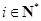 ).
).试题分析:(1)数列{bn}是等比数列,实际就是证明
 为常数,首先列出
为常数,首先列出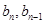 的关系式,由
的关系式,由 知消去参数
知消去参数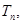 由
由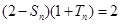 ,所以
,所以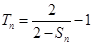 ①,当
①,当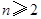 时,
时, ②,①-②,得
②,①-②,得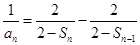 即
即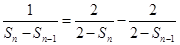 ,
,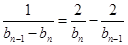 ,化简得
,化简得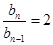 或
或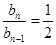 (
(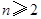 ).因为数列{an}的各项均为正数,所以数列
).因为数列{an}的各项均为正数,所以数列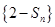 单调递减,所以
单调递减,所以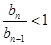 .所以
.所以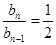 (
(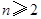 ).
).(2)由(1)知
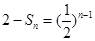 ,所以
,所以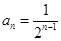 ,即
,即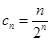 .由
.由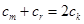 ,得
,得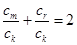 ,又
,又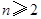 时,
时,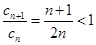 ,所以数列
,所以数列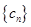 从第2项开始依次递减.当
从第2项开始依次递减.当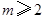 时,若
时,若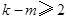 ,则
,则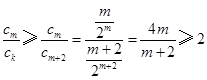 ,与
,与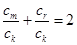 矛盾,所以
矛盾,所以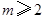 时,
时,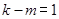 ,即
,即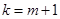 .令
.令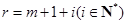 ,则
,则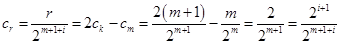 ,所以
,所以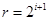 ,即存在满足题设的数组
,即存在满足题设的数组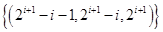 (
(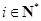 ).当
).当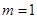 时,若
时,若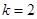 ,则
,则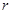 不存在;若
不存在;若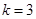 ,则
,则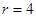 ;若
;若 时,
时,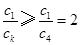 ,(*)式不成立.
,(*)式不成立.【解】(1)当
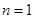 时,
时,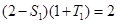 ,
,即
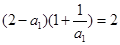 ,解得
,解得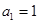 . 2分
. 2分由
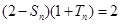 ,所以
,所以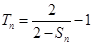 ①
① 当
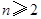 时,
时, ②
②①-②,得
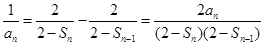 (
(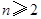 ), 4分
), 4分即
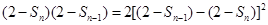 ,
,即
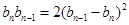 ,所以
,所以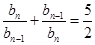 ,
,因为数列{an}的各项均为正数,所以数列
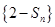 单调递减,所以
单调递减,所以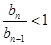 .
.所以
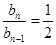 (
(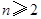 ).
).因为
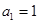 ,所以
,所以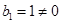 ,
,所以数列{bn}是等比数列. 6分
(2)由(1)知
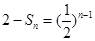 ,所以
,所以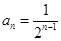 ,即
,即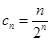 .
.由
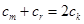 ,得
,得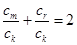 (*)
(*)又
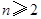 时,
时,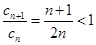 ,所以数列
,所以数列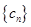 从第2项开始依次递减. 8分
从第2项开始依次递减. 8分(Ⅰ)当
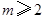 时,若
时,若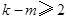 ,则
,则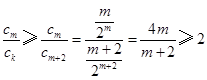 ,
,(*)式不成立,所以
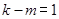 ,即
,即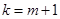 . 10分
. 10分令
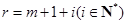 ,则
,则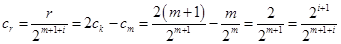 ,
,所以
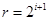 ,即存在满足题设的数组
,即存在满足题设的数组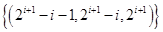 (
(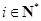 ). 13分
). 13分(Ⅱ)当
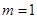 时,若
时,若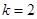 ,则
,则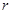 不存在;若
不存在;若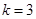 ,则
,则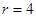 ;
;若
 时,
时,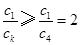 ,(*)式不成立.
,(*)式不成立.综上所述,所求集合为
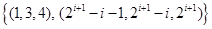 (
(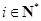 ). 16分
). 16分(注:列举出一组给2分,多于一组给3分)

练习册系列答案
相关题目
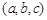 ,如下定义该数组的极差:三个数的最大值与最小值的差.如果
,如下定义该数组的极差:三个数的最大值与最小值的差.如果 ,可实施如下操作
,可实施如下操作 :若
:若 中最大的数唯一,则把最大数减2,其余两个数各增加1;若
中最大的数唯一,则把最大数减2,其余两个数各增加1;若 ,其级差为
,其级差为 .若
.若 ,则继续对
,则继续对 ,…,实施
,…,实施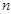 次操作后的结果记为
次操作后的结果记为 ,其极差记为
,其极差记为 .例如:
.例如: ,
,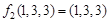 .
. ,求
,求 和
和 的值;
的值; 的极差为
的极差为 且
且 ,若
,若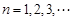 时,恒有
时,恒有 ,求
,求 的所有可能取值;
的所有可能取值;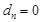 .
. 是等差数列,
是等差数列, 是等比数列,其中
是等比数列,其中 ,
, ,且
,且 为
为 、
、 的等差中项,
的等差中项, 的等差中项.
的等差中项. ,求数列
,求数列 的前
的前 项和
项和 .
. 是首项为1,公比为
是首项为1,公比为 的等比数列,若
的等比数列,若 是等差数列,则
是等差数列,则 ( )
( ) 的公差
的公差 大于0,
大于0, 是方程
是方程 的两根.
的两根.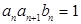 ,求数列
,求数列 的前
的前 项和.
项和.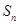 是它的前n项和.若S16>0,且
是它的前n项和.若S16>0,且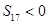 ,则当
,则当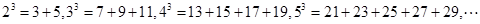 ,若类似上面各式方法将
,若类似上面各式方法将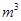 分拆得到的等式右边最后一个数是
分拆得到的等式右边最后一个数是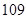 ,则正整数
,则正整数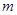 等于____.
等于____. 的前n项和为
的前n项和为 ,若
,若 ,则
,则 =__________。
=__________。