题目内容
已知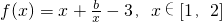 .
.
(1)b=2时,求f(x)的值域;
(2)若b为正实数,f(x)的最大值为M,最小值为m,且满足:M-m≥4,求b的取值范围.
解:(1)当b=2时,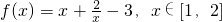 ,
,
因为f(x)在 上单调递减,在
上单调递减,在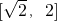 上单调递增,…(2分)
上单调递增,…(2分)
所以f(x)的最小值为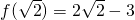 ,…(4分)
,…(4分)
又因为f(1)=f(2)=0…(5分)
所以f(x)的值域为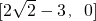 …(6分)
…(6分)
(2)①当0<b<2时,f(x)在[1,2]上单调递增,
则m=b-2,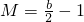 ,此时
,此时 ,得b≤-6与0<b<2矛盾(舍去)…(8分)
,得b≤-6与0<b<2矛盾(舍去)…(8分)
②当2≤b<4时,f(x)在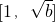 上单调递减,在
上单调递减,在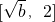 上单调递增,
上单调递增,
所以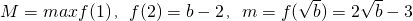 ,
,
则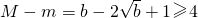 ,得
,得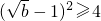 ,解得b≥9,与2≤b<4矛盾(舍去)…(11分)
,解得b≥9,与2≤b<4矛盾(舍去)…(11分)
③当b≥4时,f(x)在[1,2]上单调递减,
则M=b-2,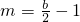 ,此时
,此时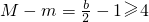 ,得b≥10…(13分)
,得b≥10…(13分)
综上所述,b的取值范围是[10,+∞)…(14分)
分析:(1)根据对勾函数的单调性看求出该函数的最小值和最大值,从而求出值域;
(2)讨论 与区间[1,2]的位置关系,然后根据函数的单调性求出f(x)的最大值为M,最小值为m,然后根据M-m≥4,求b的取值范围即可.
与区间[1,2]的位置关系,然后根据函数的单调性求出f(x)的最大值为M,最小值为m,然后根据M-m≥4,求b的取值范围即可.
点评:本题主要考查了函数的最值及其几何意义,以及函数的单调性和研究函数值域,同时考查了分类讨论的数学思想和计算能力,属于中档题.
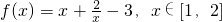 ,
,因为f(x)在
 上单调递减,在
上单调递减,在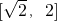 上单调递增,…(2分)
上单调递增,…(2分)所以f(x)的最小值为
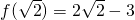 ,…(4分)
,…(4分)又因为f(1)=f(2)=0…(5分)
所以f(x)的值域为
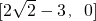 …(6分)
…(6分)(2)①当0<b<2时,f(x)在[1,2]上单调递增,
则m=b-2,
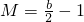 ,此时
,此时 ,得b≤-6与0<b<2矛盾(舍去)…(8分)
,得b≤-6与0<b<2矛盾(舍去)…(8分)②当2≤b<4时,f(x)在
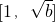 上单调递减,在
上单调递减,在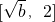 上单调递增,
上单调递增,所以
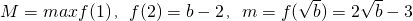 ,
,则
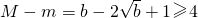 ,得
,得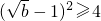 ,解得b≥9,与2≤b<4矛盾(舍去)…(11分)
,解得b≥9,与2≤b<4矛盾(舍去)…(11分)③当b≥4时,f(x)在[1,2]上单调递减,
则M=b-2,
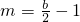 ,此时
,此时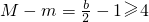 ,得b≥10…(13分)
,得b≥10…(13分)综上所述,b的取值范围是[10,+∞)…(14分)
分析:(1)根据对勾函数的单调性看求出该函数的最小值和最大值,从而求出值域;
(2)讨论
 与区间[1,2]的位置关系,然后根据函数的单调性求出f(x)的最大值为M,最小值为m,然后根据M-m≥4,求b的取值范围即可.
与区间[1,2]的位置关系,然后根据函数的单调性求出f(x)的最大值为M,最小值为m,然后根据M-m≥4,求b的取值范围即可.点评:本题主要考查了函数的最值及其几何意义,以及函数的单调性和研究函数值域,同时考查了分类讨论的数学思想和计算能力,属于中档题.

练习册系列答案
相关题目
 .
.