题目内容
已知
．
（1）b=2时，求f（x）的值域；
（2）若b为正实数，f（x）的最大值为M，最小值为m，且满足：M﹣m≥4，求b的取值范围．
．（1）b=2时，求f（x）的值域；
（2）若b为正实数，f（x）的最大值为M，最小值为m，且满足：M﹣m≥4，求b的取值范围．
解：（1）当b=2时，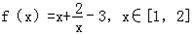
，
因为f（x）在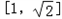
上单调递减，在
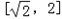上单调递增，
所以f（x）的最小值为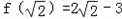
，
又因为f（1）=f（2）=0
所以f（x）的值域为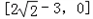
（2）①当0＜b＜2时，f（x）在[1，2]上单调递增，则
m=b﹣2，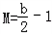
，
此时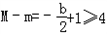
，
得b≤﹣6与0＜b＜2矛盾（舍去）
②当2≤b＜4时，f（x）在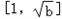
上单调递减，在
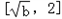上单调递增，所以
，
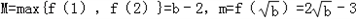则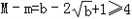
，得
，
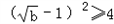解得b≥9，与2≤b＜4矛盾（舍去）
③当b≥4时，f（x）在[1，2]上单调递减，则M=b﹣2，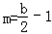
，
此时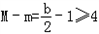
，得b≥10
综上所述，b的取值范围是[10，+∞）
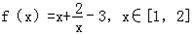，因为f（x）在
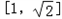上单调递减，在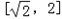上单调递增，所以f（x）的最小值为
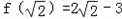，又因为f（1）=f（2）=0
所以f（x）的值域为
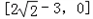
（2）①当0＜b＜2时，f（x）在[1，2]上单调递增，则
m=b﹣2，
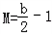，此时
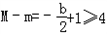，得b≤﹣6与0＜b＜2矛盾（舍去）
②当2≤b＜4时，f（x）在
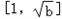上单调递减，在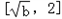上单调递增，所以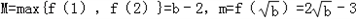，则
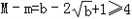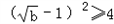，得，解得b≥9，与2≤b＜4矛盾（舍去）
③当b≥4时，f（x）在[1，2]上单调递减，则M=b﹣2，
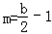，此时
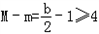，得b≥10综上所述，b的取值范围是[10，+∞）
练习册系列答案
津桥教育计算小状元系列答案
相关题目
．
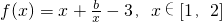