题目内容
已知平面向量| a |
| b |
| 3 |
| a |
| b |
(1)写出函数f(x)的单调递减区间;
(2)设g(x)
| lim |
| n→+∞ |
| πn |
| πn+xN |
分析:(1)用向量的数量积的坐标运算求出f(x)的解析式,整体代换的方法求出单调区间
(2)用极限的运算法则求出g(x)为分段函数,再解三角方程得交点坐标.
(2)用极限的运算法则求出g(x)为分段函数,再解三角方程得交点坐标.
解答:[理科]解:(1)f(x)=
sin(π-2x)+cos2x=2sin(2x+
),
单调递减区间为[kπ+
,kπ+
](k∈z);
(2)g(x)=
当0<x<π时,解2sin(2x+
)=1,得x=
,
当x=π时,解2sin(2x+
)=
,无解,(11分)
当π<x<2π时,解2sin(2x+
)=0,得x=
,
所以交点坐标为:(
,1),(
,0).
| 3 |
| π |
| 6 |
单调递减区间为[kπ+
| π |
| 6 |
| 2π |
| 3 |
(2)g(x)=
|
当0<x<π时,解2sin(2x+
| π |
| 6 |
| π |
| 3 |
当x=π时,解2sin(2x+
| π |
| 6 |
| 1 |
| 2 |
当π<x<2π时,解2sin(2x+
| π |
| 6 |
| 17π |
| 12 |
所以交点坐标为:(
| π |
| 3 |
| 17π |
| 12 |
点评:考查向量的数量积,极限的运算法则,三角函数的单调区间及三角方程的解法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
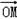 =(a,b)的“相伴函数”为f(x)=asinx+bcosx,函数f(x)=asinx+bcosx的“相伴向量”为
=(a,b)的“相伴函数”为f(x)=asinx+bcosx,函数f(x)=asinx+bcosx的“相伴向量”为 =(a,b)(其中O为坐标原点),记平面内所有向量的“相伴函数”构成的集合为S。
=(a,b)(其中O为坐标原点),记平面内所有向量的“相伴函数”构成的集合为S。 )+4sinx,求证:g(x)∈S;
)+4sinx,求证:g(x)∈S; 的“相伴函数”f(x)在x=x0处取得最大值,当点M在圆C上运动时,求tan2x0的取值范围。
的“相伴函数”f(x)在x=x0处取得最大值,当点M在圆C上运动时,求tan2x0的取值范围。 =(a,b)的“相伴函数”为f(x)=asinx+bcosx,函数f(x)=asinx+bcosx的“相伴向量”为
=(a,b)的“相伴函数”为f(x)=asinx+bcosx,函数f(x)=asinx+bcosx的“相伴向量”为 =(a,b)(其中O为坐标原点).记平面内所有向量的“相伴函数”构成的集合为S.
=(a,b)(其中O为坐标原点).记平面内所有向量的“相伴函数”构成的集合为S. )+4sinx,求证:g(x)∈S;
)+4sinx,求证:g(x)∈S; 的“相伴函数”f(x)在x=x处取得最大值.当点M在圆C上运动时,求tan2x的取值范围.
的“相伴函数”f(x)在x=x处取得最大值.当点M在圆C上运动时,求tan2x的取值范围.