题目内容
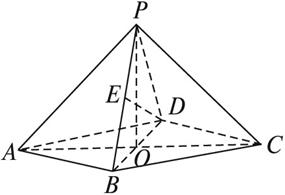
在四棱锥P—ABCD中,底面是边长为2的菱形,∠DAB=60°,对角线AC与BD相交于点O,PO⊥平面ABCD,PB与平面ABCD所成角为60°.(1)求四棱锥P—ABCD的体积;
(2)若E是PB的中点,求异面直线DE与PA所成角的余弦值.
解:(1)∵ABCD是边长为2的菱形,且∠DAB=60°,
∴OA=OC=![]() ,BO=OD=1,
,BO=OD=1,
S菱形ABCD=![]()
在Rt△POB中,∠PBO=60°,PO=tan60°·1=![]() .
.
∴VP-ABCD=![]() SABCD·PO=
SABCD·PO=![]() ×2
×2![]() ×
×![]() =2.
=2.
(2)以O为原点,OB、OC、OP分别为x轴、y轴、z轴建立空间直角坐标系,则
B(1,0,0),C(0,![]() ,0),D(-1,0,0),A(0,-
,0),D(-1,0,0),A(0,-![]() ,0),P(0,0,
,0),P(0,0,![]() ).
).
于是E(![]() ).
).
![]()
∴cos〈![]() 〉=
〉=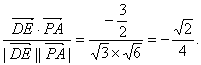

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
 如图,在四棱锥P-ABCD中,底面为直角梯形,AD∥BC,∠BAD=90,PA⊥底面ABCD,且PA=AD=AB=2BC=2,M,N分别为PC、PB的中点.
如图,在四棱锥P-ABCD中,底面为直角梯形,AD∥BC,∠BAD=90,PA⊥底面ABCD,且PA=AD=AB=2BC=2,M,N分别为PC、PB的中点. 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4.AB=2,AN⊥PC于点N,M是PD中点.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4.AB=2,AN⊥PC于点N,M是PD中点. 如图,在四棱锥P-ABCD中,底面ABCD是矩形,O为底面中心,PA⊥平面ABCD,PA=AD=2AB.M是PD的中点
如图,在四棱锥P-ABCD中,底面ABCD是矩形,O为底面中心,PA⊥平面ABCD,PA=AD=2AB.M是PD的中点 如图,在四棱锥P-ABCD中,底面ABCD是矩形,已知AB=3,AD=2,PA=2,PD=2
如图,在四棱锥P-ABCD中,底面ABCD是矩形,已知AB=3,AD=2,PA=2,PD=2 (2009•成都模拟)如图,在四棱锥P-ABCD中,底面ABCD为正方形,且PD⊥平面ABCD,PD=AB=1,EF分别是PB、AD的中点,
(2009•成都模拟)如图,在四棱锥P-ABCD中,底面ABCD为正方形,且PD⊥平面ABCD,PD=AB=1,EF分别是PB、AD的中点,