题目内容
(本小题满分12分)
各项均为正数的数列 的前
的前 项和为
项和为 ,已知点
,已知点 在函数
在函数 的图象上,且
的图象上,且
(I)求数列 的通项公式;
的通项公式;
(II)在 之间插入
之间插入 个数,使这
个数,使这 个数组成公差为
个数组成公差为 的等差数列,求数列
的等差数列,求数列 的前
的前 项和
项和 .
.
(Ⅰ) ; (Ⅱ)
; (Ⅱ)
【解析】
试题分析:(Ⅰ)首先根据已知条件,可得 ,所以
,所以 ,进而求出数列
,进而求出数列 的通项公式.(Ⅱ)由
的通项公式.(Ⅱ)由 ,
, ,可得
,可得 ,利用错位相减法即可求出数列
,利用错位相减法即可求出数列 的前
的前 项和
项和 .
.
试题解析:【解析】
(Ⅰ)由题意可知, ,所以数列
,所以数列 是公比为3的等比数列
是公比为3的等比数列
∵ ,
,
∴ ,解得
,解得 ,
,
∴数列 的通项公式
的通项公式 .
.
(Ⅱ)由(Ⅰ)知 ,
,
∵ ,
,
∴ ,
,
∴
 ,①
,①
 ,②
,②
①-②,得:


 ,
,
∴ .
.
考点:1. 数列递推式;2.等比数列;3. 数列的求和.

练习册系列答案
相关题目
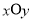 中,曲线
中,曲线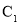 的参数方程为
的参数方程为 (
(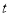 为参数),以原点
为参数),以原点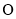 为极点,以
为极点,以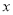 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线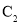 的极坐标方程为
的极坐标方程为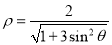 .
. 求曲线
求曲线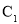 的普通方程与曲线
的普通方程与曲线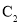 的直角坐标方程;
的直角坐标方程;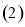 试判断曲线
试判断曲线 与
与 是否存在两个交点,若存在,求出两交点间的距离;若不存在,说明理由.
是否存在两个交点,若存在,求出两交点间的距离;若不存在,说明理由.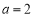 ”是“直线
”是“直线 和
和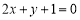 互相平行”的 ( )
互相平行”的 ( ) 的动弦
的动弦 的长为
的长为 ,则弦
,则弦 到
到 轴的最短距离是 .
轴的最短距离是 .  是等差数列
是等差数列 的前
的前 项和,若
项和,若 ,则
,则 .
.  分别为双曲线
分别为双曲线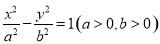 的左,右焦点,P为双曲线右支上的一点,且
的左,右焦点,P为双曲线右支上的一点,且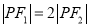 .若
.若 为等腰三角形,则该双曲线的离心率为_________.
为等腰三角形,则该双曲线的离心率为_________. ,则黄豆落入阴影部分的概率为( )
,则黄豆落入阴影部分的概率为( )




 的部分图象如图所示,则在
的部分图象如图所示,则在 上,下列函数中与
上,下列函数中与 的单调性不同的是
的单调性不同的是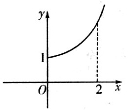
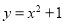 B.
B. 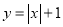
 D.
D. 
 是方程
是方程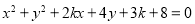 表示圆的充要条件;
表示圆的充要条件;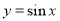 的图象向右平移
的图象向右平移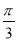 单位,再保持纵坐标不变,横坐标变为原来的
单位,再保持纵坐标不变,横坐标变为原来的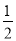 ,得到函数
,得到函数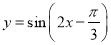 的图象;
的图象;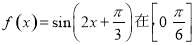 上为增函数;
上为增函数;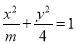 的焦距为2,则实数m的值等于5.
的焦距为2,则实数m的值等于5.