题目内容
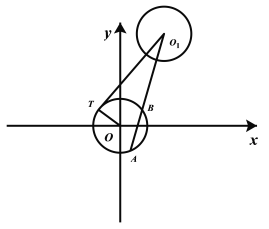
【题目】已知在平面直角坐标系中，圆
的参数方程为
（
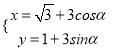为参数），以原点为极点，以
轴为非负半轴为极轴建立极坐标系.
（1）求圆
的普通方程与极坐标方程；
（2）若直线
的极坐标方程为
，求圆
上的点到直线
的最大距离.
【答案】(1)普通方程为
，极坐标方程为
.(2)5.
【解析】试题分析:（1）先根据同角三角函数关系消参数可得圆
的普通方程，再利用
将直角坐标方程化为极坐标方程（2）先根据
将直线
的极坐标方程化为直角坐标方程，再根据圆的几何条件得圆
上的点到直线
的最大距离为圆心到直线距离减去半径，最后根据点到直线距离公式求最值
试题解析：（1）圆
的圆心
为
，半径
，
则普通方程为
，
其极坐标方程为
，
即
（2）由
得
，
化为
，即
，
圆心
到直线
的距离为
，
故圆
上的点到直线
的最大距离为
.
练习册系列答案
相关题目
【题目】语音交互是人工智能的方向之一，现在市场上流行多种可实现语音交互的智能音箱，它们可以通过语音交互满足人们的部分需求.经市场调查，某种新型智能音箱的广告费支出x（万元）与销售额y（单位：万元）之间有如下对应数据：
x | 1 | 4 | 5 | 6 | 9 |
y | 20 | 35 | 50 | 65 | 80 |
（1）求y关于x的线性回归方程（数据精确到0.01）；
（2）利用（1）中的回归方程，预测广告费支出10万元时的销售额.
附：回归直线的斜率和截距的最小二乘估计公式分别为：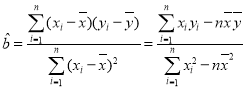
，
.
