题目内容
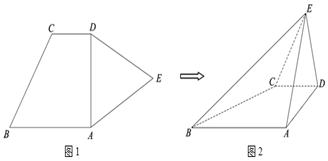
12.如图1,平面五边形ABCDE中,AB∥CD,∠BAD=90°,AB=2,CD=1,△ADE是边长为2的正三角形.现将△ADE沿AD折起,得到四棱锥E-ABCD(如图2),且DE⊥AB.(Ⅰ)求证:平面ADE⊥平面ABCD;
(Ⅱ)求平面BCE和平面ADE所成锐二面角的大小;
(Ⅲ)在棱AE上是否存在点F,使得DF∥平面BCE?若存在,求$\frac{EF}{EA}$的值;若不存在,请说明理由.
分析 (Ⅰ)推导出AB⊥AD,AB⊥DE,从而AB⊥平面ADE,由此能平面ADE⊥平面ABCD.
(Ⅱ)设AD的中点为O,连接EO,推导出EO⊥AD,从而EO⊥平面ABCD.以O为原点,OA所在的直线为x轴,在平面ABCD内过O 垂直于AD的直线为y轴,OE所在的直线为z轴,建立空间直角坐标系O-xyz,利用向量法能求出平面BCE和平面ADE所成的锐二面角大小.
(Ⅲ)设BE的中点为G,连接CG,FG,推导出四边形CDFG是平行四边形,从而DF∥CG.由此能求出在棱AE上存在点F,使得DF∥平面BCE,此时$\frac{EF}{EA}=\frac{1}{2}$.
解答 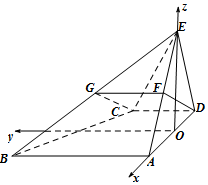 (本小题共14分)
(本小题共14分)
证明:(Ⅰ)由已知得AB⊥AD,AB⊥DE.
因为AD∩DE=D,所以AB⊥平面ADE.
又AB?平面ABCD,所以平面ADE⊥平面ABCD..…(4分)
解:(Ⅱ)设AD的中点为O,连接EO.
因为△ADE是正三角形,所以EA=ED,所以EO⊥AD.
因为 平面ADE⊥平面ABCD,
平面ADE∩平面ABCD=AD,EO?平面ADE,
所以EO⊥平面ABCD.
以O为原点,OA所在的直线为x轴,在平面ABCD内过O 垂直于AD的直线为y轴,OE所在的直线为z轴,
建立空间直角坐标系O-xyz,如图所示.
由已知,得E(0,0,$\sqrt{3}$),B(1,2,0),C(-1,1,0).
所以$\overrightarrow{CE}$=(1,-1,$\sqrt{3}$),$\overrightarrow{CB}$=(2,1,0).
设平面BCE的法向量$\overrightarrow{m}$=(x,y,z).
则 $\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{CE}=x-y+\sqrt{3}z=0}\\{\overrightarrow{m}•\overrightarrow{CB}=2x+y=0}\end{array}\right.$,
令x=1,则$\overrightarrow{m}$=(1,-2,-$\sqrt{3}$).
又平面ADE的一个法向量$\overrightarrow{n}$=(0,1,0),
所以cos<$\overrightarrow{m},\overrightarrow{n}$>=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}|•|\overrightarrow{n}|}$=-$\frac{\sqrt{2}}{2}$.
所以平面BCE和平面ADE所成的锐二面角大小为$\frac{π}{4}$.…(10分)
(Ⅲ)在棱AE上存在点F,使得DF∥平面BCE,此时$\frac{EF}{EA}=\frac{1}{2}$.
理由如下:
设BE的中点为G,连接CG,FG,
则FG∥AB,FG=$\frac{1}{2}AB$.
因为AB∥CD,且$CD=\frac{1}{2}AB$,所以FG∥CD,且FG=CD,
所以四边形CDFG是平行四边形,所以DF∥CG.
因为CG?平面BCE,且DF?平面BCE,
所以DF∥平面BCE..…(14分)
点评 本题考查面面垂直的证明,考查二面角的求法,考查满足线面平行的点是否存在的判断与求法,考查推理论证能力、运算求解能力、空间思维能力,考查数形结合思想、转化化归思想,是中档题.

 同步练习强化拓展系列答案
同步练习强化拓展系列答案| A. | ?x0∉[0,+∞),${e^{x_0}}<1$ | B. | ?x∉[0,+∞),ex<1 | ||
| C. | ?x0∈[0,+∞),${e^{x_0}}<1$ | D. | ?x∈[0,+∞),ex<1 |
| A. | $(\frac{π}{2},π)$ | B. | $(\frac{π}{4},\frac{3π}{4})$ | C. | $(π,\frac{3π}{2})$ | D. | $(\frac{3π}{4},\frac{5π}{4})$ |
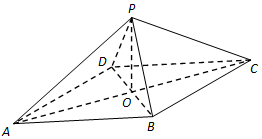 如图,在四棱锥P-ABCD中,四边形ABCD是平行四边形,AD⊥BD且AD=BD,AC∩BD=O,PO⊥平面ABCD.
如图,在四棱锥P-ABCD中,四边形ABCD是平行四边形,AD⊥BD且AD=BD,AC∩BD=O,PO⊥平面ABCD.