Question

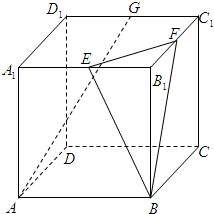如图，在棱长为1的正方体ABCD-A₁B₁C₁D₁中，E，F，G分别为A₁B₁、B₁C₁、C₁D₁的中点．
（1）求异面直线AG与BF所成角的余弦值；
（2）求证：AG∥平面BEF；
（3）试在棱BB₁上找一点M，使DM⊥平面BEF，并证明你的结论．

Answer 1

分析：（1）建立空间直角坐标系，可得

AG

=(-1，

1

2

，1)，

BF

=(-

1

2

，0，1)，进而利用向量的有关运算计算出两个向量的夹角，再转化为两条异面直线的夹角．
（2）利用向量的关系可得：

AG

=

EF

+

BF

，所以

AG

与平面BEF共面，再根据线面平行的判定定理可得答案．
（3）因为DM⊥平面BEF，所以

DM

•

EF

=0，

DM

•

BF

=0，进而求出m的数值得到答案．

解答：解：（1）以D为坐标原点，DA，DC，DD₁分别作为x轴，y轴和z轴建立空间直角坐标系，
则A（1，0，0），B（1，1，0），E(1，

1

2

，1)，F(

1

2

，1，1)，G(0，

1

2

，1)，
∴

AG

=(-1，

1

2

，1)，

BF

=(-

1

2

，0，1)，
∴cos＜

AG

，

BF

＞=

3 2

3 2 • 5 2

=

2 5

5

故异面直线AG与BF所成角的余弦值为

2 5

5

．
（2）∵

EF

=(-

1

2

，

1

2

，0)，

BF

=(-

1

2

，0，1)，
而

AG

=(-1，

1

2

，1)，∴

AG

=

EF

+

BF

，
故

AG

与平面BEF共面，
又因为AG不在平面BEF内，
∴AG∥平面BEF．
（3）设M（1，1，m），则

DM

=(1，1，m)
由

DM

•

EF

=0，

DM

•

BF

=0，
∴-

1

2

+m=0?m=

1

2

，
所以M为棱BB₁的中点时，DM⊥平面BEF．

点评：解决此类问题的关键是熟练掌握几何体的结构特征，建立空间直角坐标系以便利用向量的有关知识解决线面关系与空间角等问题．