题目内容
设抛物线![]() 的准线与
的准线与![]() 轴交点为
轴交点为![]() ,过点
,过点![]() 作直线
作直线![]() 交抛物线与不同的点
交抛物线与不同的点![]() 两点.
两点.
(1)求线段![]() 中点的轨迹方程;
中点的轨迹方程;
(2)若线段![]() 的垂直平分线交抛物线对称轴与
的垂直平分线交抛物线对称轴与![]() ,求证:
,求证:![]() .
.
(Ⅰ)![]() (Ⅱ)见解析
(Ⅱ)见解析
解析:
(1)![]() 的准线为
的准线为![]() 故点M的坐标为
故点M的坐标为![]()
设直线AB的方程为![]() 代入
代入![]() 得
得
![]()
设线段AB的中点为![]() 则
则
 即
即![]()
 消去
消去![]() 得:
得:
![]()
![]() 线段
线段![]() 中点的轨迹方程为
中点的轨迹方程为![]() .
.
(2)证明:抛物线![]() 对称轴为
对称轴为![]() 轴
轴
AB中点为(![]() ,
,![]() )线段AB中垂线斜率为
)线段AB中垂线斜率为![]()
故线段AB的中垂线方程为![]()
令![]() 得
得![]() 由(1)可知交点AB存在则
由(1)可知交点AB存在则![]() 故
故![]()

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目

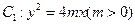 的准线与
的准线与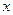 轴交于
轴交于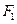 ,焦点为
,焦点为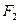 ;以
;以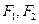 为焦点,离心率
为焦点,离心率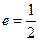 的椭圆
的椭圆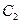 与抛物线
与抛物线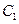 在
在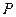 ,延长
,延长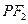 交抛物线于点
交抛物线于点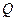 ,
,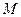 是抛物线
是抛物线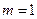 时,求椭圆
时,求椭圆 的边长恰好是三个连续的自然数时,求
的边长恰好是三个连续的自然数时,求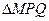 面积的最大值.
面积的最大值.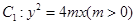 的准线与
的准线与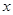 轴交于
轴交于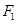 ,焦点为
,焦点为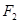 ;以
;以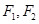 为焦点,离心率
为焦点,离心率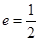 的椭圆
的椭圆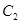 与抛物线
与抛物线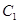 在
在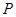 ,延长
,延长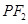 交抛物线于点
交抛物线于点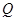 ,
,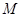 是抛物线
是抛物线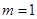 时,求椭圆
时,求椭圆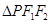 的边长恰好是三个连续的自然数时,
的边长恰好是三个连续的自然数时,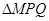 面积的最大值.
面积的最大值.
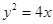 的准线与
的准线与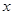 轴交于
轴交于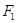 ,焦点为
,焦点为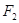 ,以
,以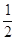 的椭圆的两条准线之间的距离为
的椭圆的两条准线之间的距离为