题目内容
若函数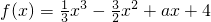 ,恰在[-1,4]上递减,则实数a的取值范围是________.
,恰在[-1,4]上递减,则实数a的取值范围是________.
{x|x=-4}
分析:原函数是一个三次多项式函数,因此考虑用导函数的方法研究它的单调性.先求出f′(x)=x2-3x+a,函数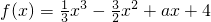 ,恰在[-1,4]上递减,说明f′(x)≤0的解集恰好是[-1,4],最后利用一元二次方程根与系数的关系,可得出实数a的取值范围.
,恰在[-1,4]上递减,说明f′(x)≤0的解集恰好是[-1,4],最后利用一元二次方程根与系数的关系,可得出实数a的取值范围.
解答:先求出f′(x)=x2-3x+a,
∵函数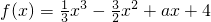 ,恰在[-1,4]上递减,
,恰在[-1,4]上递减,
∴不等式f′(x)≤0的解集恰好是[-1,4],
也就是说:方程x2-3x+a=0的根是x1=-1,x2=4
用一元二次方程根与系数的关系,得: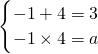
所以a=-4
故答案为:{x|x=-4}
点评:本题以三次多项式函数为例,考查了利用导数研究函数的单调性,属于中档题.深刻理解一元二次不等式的解集与一元二次方程根之间的关系,是解决好本题的关键.
分析:原函数是一个三次多项式函数,因此考虑用导函数的方法研究它的单调性.先求出f′(x)=x2-3x+a,函数
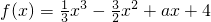 ,恰在[-1,4]上递减,说明f′(x)≤0的解集恰好是[-1,4],最后利用一元二次方程根与系数的关系,可得出实数a的取值范围.
,恰在[-1,4]上递减,说明f′(x)≤0的解集恰好是[-1,4],最后利用一元二次方程根与系数的关系,可得出实数a的取值范围.解答:先求出f′(x)=x2-3x+a,
∵函数
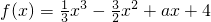 ,恰在[-1,4]上递减,
,恰在[-1,4]上递减,∴不等式f′(x)≤0的解集恰好是[-1,4],
也就是说:方程x2-3x+a=0的根是x1=-1,x2=4
用一元二次方程根与系数的关系,得:
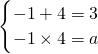
所以a=-4
故答案为:{x|x=-4}
点评:本题以三次多项式函数为例,考查了利用导数研究函数的单调性,属于中档题.深刻理解一元二次不等式的解集与一元二次方程根之间的关系,是解决好本题的关键.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目