题目内容
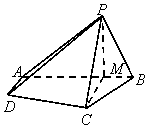
在四棱锥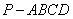 中,
中, 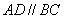 ,
,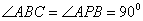 ,点
,点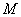 是线段
是线段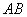 上的一点,且
上的一点,且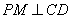 ,
, .
.
(1)证明:面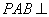 面
面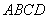 ;
;
 (2)求直线
(2)求直线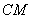 与平面
与平面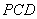 所成角的正弦值.
所成角的正弦值.
解(1)由 ,得
,得 ,
,
又因为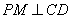 ,且
,且 ,所以
,所以 面
面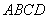 ,
,
且 面
面 .所以,面
.所以,面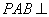 面
面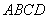 。
。
(2)过点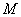 作
作 ,连结
,连结 ,
,
因为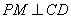 ,且
,且 ,
,
所以 平面
平面 ,又由
,又由 平面
平面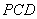 ,
,
所以平面 平面
平面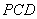 ,平面
,平面 平面
平面 ,过点
,过点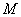 作
作 ,
,
即有 平面
平面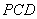 ,所以
,所以 为直线
为直线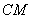 与平面
与平面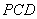 所成角.
所成角.
在四棱锥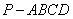 中,设
中,设 ,则
,则 ,
, ,
, ,∴
,∴ ,
, ,从而
,从而 ,即直线
,即直线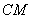 与平面
与平面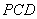 所成角的正弦值为
所成角的正弦值为 .
.

练习册系列答案
相关题目
 B.-1 C.0 D.1
B.-1 C.0 D.1 ,下面四个等式中,正确的命题为______________________________________.①
,下面四个等式中,正确的命题为______________________________________.① ;②
;② ;③
;③ ;④
;④ ;
; ,集合
,集合 .
. ;
; ,
, ,求实数
,求实数 的取值范围.
的取值范围. 如图为函数
如图为函数 的图象(
的图象( 均为实常数),
均为实常数),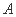 )
) (
(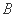 )
)
 )
) (
( )
)
