题目内容
过点M(3,4),倾斜角为
的直线l与圆C:
(θ为参数)相交于A、B两点,试确定|MA|•|MB|的值.
| π |
| 6 |
|
分析:先求得直线l的参数方程、圆C的普通方程,再把直线的参数方程代入圆C的普通方程化简可得 t2+(3+
)t-15,再由|MA|•|MB|=|t1•t2|,求得结果.
| 3 |
解答:解:过点M(3,4),倾斜角为
的直线l的参数方程为
,
圆C:
(θ为参数),即(x-2)2+(y-1)2=25.
把直线的参数方程代入圆C的方程化简可得 t2+(3+
)t-15=0,
∴|MA|•|MB|=|t1|•|t2|=|t1•t2|=15.
| π |
| 6 |
|
圆C:
|
把直线的参数方程代入圆C的方程化简可得 t2+(3+
| 3 |
∴|MA|•|MB|=|t1|•|t2|=|t1•t2|=15.
点评:本题主要考查求直线的参数方程,把参数方程化为普通方程,参数的几何意义,属于基础题.

练习册系列答案
相关题目
 的直线
的直线 与圆C:
与圆C: (
( 为参数)相交于A、B两点,试确定
为参数)相交于A、B两点,试确定 的值.
的值. 及对应的一个特征向量
及对应的一个特征向量 ,并且矩阵M对应的变换将点
,并且矩阵M对应的变换将点 变换成
变换成 ,求矩阵M。
,求矩阵M。 的直线
的直线 与圆C:
与圆C: (
( 为参数)相交于A、B两点,试确定
为参数)相交于A、B两点,试确定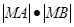 的值。
的值。 满足
满足 ,
, ,试确定
,试确定 的最大值。
的最大值。