题目内容
已知椭圆(Ⅰ)求椭圆C的方程;
(Ⅱ)已知过点F1(-2,0)倾斜角为![]() 的直线交椭圆C于A,B两点.
的直线交椭圆C于A,B两点.
求证:![]()
(Ⅲ)过点F1(-2,0)作两条互相垂直的直线分别交椭圆C于点A、B和D、E,求![]() 的最小值.
的最小值.
本题主要考查直线的方程、椭圆的方程和性质、直线与椭圆的位置关系的知识.考查数形结合的数学思想以及运算能力和综合解题能力.
解 :(1)由题意得:

![]() 椭圆
椭圆![]() 的方程为
的方程为![]()
(2)方法一:
由(1)知![]() 是椭圆
是椭圆![]() 的左焦点,离心率
的左焦点,离心率![]()
设![]() 为椭圆的左准线。则
为椭圆的左准线。则![]()
作![]() ,
,![]() 与
与![]() 轴交于点H(如图)
轴交于点H(如图)
![]() 点A在椭圆上
点A在椭圆上
![]()
![]()
![]()
![]()
同理 ![]()
![]() 。
。

方法二:
当![]() 时,记
时,记![]() ,则
,则![]()
将其代入方程 ![]() 得
得 ![]()
设 ![]() ,则
,则![]() 是此二次方程的两个根.
是此二次方程的两个根.
![]()
![]()
![]() ................(1)
................(1)
![]() 代入(1)式得
代入(1)式得 ![]() ........................(2)
........................(2)
当![]() 时,
时,![]() 仍满足(2)式。
仍满足(2)式。
![]()
(3)设直线![]() 的倾斜角为
的倾斜角为![]() ,由于
,由于![]() 由(2)可得
由(2)可得
![]() ,
,![]()

当![]() 时,
时,![]() 取得最小值
取得最小值![]()

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
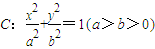 ,其相应于焦点F(2,0)的准线方程为x=4.
,其相应于焦点F(2,0)的准线方程为x=4.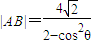 ;
;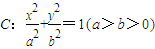 ,其相应于焦点F(2,0)的准线方程为x=4.
,其相应于焦点F(2,0)的准线方程为x=4.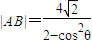 ;
;