题目内容
双曲线的方程为
-
=1,以它的右焦点为圆心,作过原点O的圆,求此圆与双曲线相交的公共弦之长.
公共弦|AB|=
.
解析:
由题意可知,圆的方程为(x-3)2+y2=9与双曲线交于两点A、B.
又∵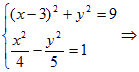
9x2-24x-20=0,设A(x1,y1)、B(x2,y2).
∴x1=-
(舍),x2=
.
则y1=±
.
∴公共弦|AB|=
.
练习册系列答案
53随堂测系列答案
相关题目
解析:
53随堂测系列答案题目内容
双曲线的方程为-=1,以它的右焦点为圆心,作过原点O的圆,求此圆与双曲线相交的公共弦之长.
公共弦|AB|=.
由题意可知,圆的方程为(x-3)2+y2=9与双曲线交于两点A、B.
又∵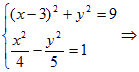9x2-24x-20=0,设A(x1,y1)、B(x2,y2).
∴x1=-(舍),x2=.
则y1=±.
∴公共弦|AB|=.
53随堂测系列答案
+
=1,点A、B在双曲线的右支上，线段AB经过双曲线的右焦点F2，|AB|=m,F1为另一焦点，则△ABF1的周长为（ ） 
-
=1,点A、B在双曲线的右支上，线段AB经过双曲线的右焦点F2，|AB|=m，F1为另一焦点，则△ABF1的周长为( )
-
=1,过其右焦点作一条垂直于x轴的直线与此双曲线交于A、B两点,则|AB|的长为（ ）
-
=1,点A、B在双曲线的右支上，线段AB经过双曲线的右焦点F2，|AB|=m,F1为另一焦点，则△ABF1的周长为( )