题目内容

对于函数y=|lgx|，若存在0＜a＜b，且f（a）=f（b），则a+b的取值范围为________．

（2，+∞）

分析：由f（a）=f（b）且0＜a＜b可得f（a）＜0，f（b）＞0．且-lg（a）=lg（b），从而可得ab=1，由0＜a＜b可得0＜a＜1＜b
（法一）：由基本不等式可得，a+b＞2 $\text{[math]}$ 可求
（法二）：由于 $\text{[math]}$ ，在（0，1）上单调递减，从而可求
解答：由f（a）=f（b）且0＜a＜b可得f（a）＜0，f（b）＞0．且-lg（a）=lg（b）
∴lgab=0
∴ab=1
由0＜a＜b可得0＜a＜1＜b
（法一）：由基本不等式可得，a+b＞2 $\text{[math]}$
（法二）：∵ $\text{[math]}$ ，在（0，1）上单调递减
∴ $\text{[math]}$

∴a+b＞2
故答案为：（2，+∞）
点评：本题主要考查了对数函数的单调性及对数运算性质的应用，还考查了基本不等式及函数y=x+ $\text{[math]}$ 的单调性在求解最值中的应用．

练习册系列答案

课课练与单元测试系列答案

世纪金榜小博士单元期末一卷通系列答案

单元测试AB卷台海出版社系列答案

黄冈新思维培优考王单元加期末卷系列答案

名校名师夺冠金卷系列答案

小学英语课时练系列答案

培优新帮手系列答案

天天向上一本好卷系列答案

小学生10分钟应用题系列答案

课堂作业广西教育出版社系列答案

相关题目

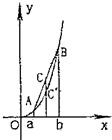如图，对于函数f（x）=x³（x＞0）上任意两点A（a，a³），B（b，b³）线段AB在弧线段AB的上方，

，则由图中点C在C’上方可得不等式

)3，请分析函数y=lgx（x＞0）的图象，类比上述不等式可以得到的不等式是

给出下列五个命题：
①函数y=f（x），x∈R的图象与直线x=a可能有两个不同的交点；
②函数y=log₂x²与函数y=2log₂x是相等函数；
③对于指数函数y=2^x与幂函数y=x²，总存在x₀，当x＞x₀ 时，有2^x＞x²成立；
④对于函数y=f（x），x∈[a，b]，若有f（a）•f（b）＜0，则f（x）在（a，b）内有零点．
⑤已知x₁是方程x+lgx=5的根，x₂是方程x+10^x=5的根，则x₁+x₂=5．
其中正确的序号是

对于函数y=f（x），x∈D，若存在常数c，使对任意x₁∈D，存在唯一的x₂∈D，满足

=c，则称函数f（x）在D上的均值为c，现已知函数：①y=2^x，②y=x⁵，③y=2sinx，④y=lgx，则满足在其定义域上均值为2的函数的序号是

（填上所有符合要求的函数的序号）

给出下列五个命题：
①函数y=f（x），x∈R的图象与直线x=a可能有两个不同的交点；
②函数y=log₂x²与函数y=2log₂x是相等函数；
③对于指数函数y=2^x与幂函数y=x²，总存在x，当x＞x 时，有2^x＞x²成立；
④对于函数y=f（x），x∈[a，b]，若有f（a）•f（b）＜0，则f（x）在（a，b）内有零点．
⑤已知x₁是方程x+lgx=5的根，x₂是方程x+10^x=5的根，则x₁+x₂=5．
其中正确的序号是．