题目内容
抛物线顶点在原点,焦点在x轴上,且过点(8,8),焦点为F(1)求抛物线的焦点坐标和标准方程;
(2)P是抛物线上一动点,M是PF的中点,求M的轨迹方程.
【答案】分析:(1)先设出抛物线方程,因为抛物线过点(8,8),所以点(8,8)的坐标满足抛物线方程,就可求出抛物线的标准方程,得到抛物线的焦点坐标.
(2)利用相关点法求PF中点M的轨迹方程,先设出M点的坐标为(x,y),P点坐标为(x,y),把P点坐标用M点的坐标表示,再代入P点满足的方程,化简即可得到M点的轨迹方程.
解答:解:(1)抛物线顶点在原点,焦点在x轴上,且过点(8,8),
设抛物线解析式为y2=2px,把(8,8)代入,得,64=2×8p,∴p=4
∴抛物线标准方程为:y2=8x,焦点坐标为F(2,0)
(2)设M(x,y),P(x,y),
由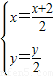 ⇒
⇒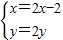
又∵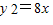 ,
,
∴(2y)2=8(2x-2)
∴y2=4(x-1)
∴M的轨迹方程为 y2=4x-4.
点评:本题主要考查了抛物线的标准方程的求法,以及相关点法求轨迹方程,属于解析几何的常规题.
(2)利用相关点法求PF中点M的轨迹方程,先设出M点的坐标为(x,y),P点坐标为(x,y),把P点坐标用M点的坐标表示,再代入P点满足的方程,化简即可得到M点的轨迹方程.
解答:解:(1)抛物线顶点在原点,焦点在x轴上,且过点(8,8),
设抛物线解析式为y2=2px,把(8,8)代入,得,64=2×8p,∴p=4
∴抛物线标准方程为:y2=8x,焦点坐标为F(2,0)
(2)设M(x,y),P(x,y),
由
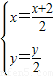 ⇒
⇒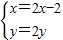
又∵
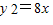 ,
,∴(2y)2=8(2x-2)
∴y2=4(x-1)
∴M的轨迹方程为 y2=4x-4.
点评:本题主要考查了抛物线的标准方程的求法,以及相关点法求轨迹方程,属于解析几何的常规题.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
相关题目
 抛物线有光学性质:由其焦点射出的光线经抛物线反象后,沿平行于抛物线对称轴的肖向射出,反之亦然.如图所示,今有抛物线C,其顶点是坐标原点,对称辅为x轴.开口向右.一光源在点M处,由其发出一条平行于x轴的光线射向抛物线C卜的点P(4.4),经抛物线C反射后,反射光线经过焦点F后射向抛物线C上的点Q,再经抛物线C反射后又沿平行于X轴的方向射出,途中经直线l:2x-4y-17=0上点N反射后又射回点M.
抛物线有光学性质:由其焦点射出的光线经抛物线反象后,沿平行于抛物线对称轴的肖向射出,反之亦然.如图所示,今有抛物线C,其顶点是坐标原点,对称辅为x轴.开口向右.一光源在点M处,由其发出一条平行于x轴的光线射向抛物线C卜的点P(4.4),经抛物线C反射后,反射光线经过焦点F后射向抛物线C上的点Q,再经抛物线C反射后又沿平行于X轴的方向射出,途中经直线l:2x-4y-17=0上点N反射后又射回点M.
