题目内容
材料:

在物理学习中,知道一个物体受到力的作用,如果在力的方向上发生一段位移,这个力就对物体做了功.而力对物体所做的功,等于力的大小、位移的大小、力和位移的夹角的余弦这三者的乘积.若设力和位移的夹角为α,则当α=![]() 时,cosα=0,此时力对物体所做功为零,如图(1)重力和支持力对物体所做的功为零;当0≤α<
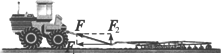
时,cosα=0,此时力对物体所做功为零,如图(1)重力和支持力对物体所做的功为零;当0≤α<![]() 时,cosα>0,此时力对物体所做的功为正功,如图(2)人用力拉车前进,此时拉开力对车所做为正功;当π≥α>
时,cosα>0,此时力对物体所做的功为正功,如图(2)人用力拉车前进,此时拉开力对车所做为正功;当π≥α>![]() 时,cosα<0,此时力对物体所做的功为负功,如图(3),人向后拉车的力对车所做功为负功.力与位移都是向量,而功则可以抽象为数学中向量的数量积.
时,cosα<0,此时力对物体所做的功为负功,如图(3),人向后拉车的力对车所做功为负功.力与位移都是向量,而功则可以抽象为数学中向量的数量积.
由上面的这段话,你能不能概括出向量数量积的定义?并且说出何时向量的数量积是正值?何时是负值?何时是零?
答案:
解析:
解析:
|
力和位移对应于数学中的向量,它们的大小对应于数学中的向量的模,力和位移的夹角则对应于数学中两个向量的夹角,由此可知两个向量的数量积等于这两个向量的模与它夹角余弦值之积,而这个积的正负则取决于这两个向量的夹角的大小. |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目