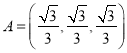题目内容
【题目】设![]() 数列
数列![]() 的前
的前![]() 项和,对任意
项和,对任意![]() ,都有
,都有![]() (
(![]() 为常数).
为常数).
(1)当![]() 时,求
时,求![]() ;
;
(2)当![]() 时,
时,
(ⅰ)求证:数列![]() 是等差数列;
是等差数列;
(ⅱ)若对任意![]() ,必存在
,必存在![]() 使得
使得![]() ,已知
,已知![]() ,且
,且![]() ,求数列
,求数列![]() 的通项公式.
的通项公式.
【答案】(1) ![]() .
.
(2) (ⅰ)证明见解析;(ⅱ)![]() .
.
【解析】
(1)利用项和公式求出![]() 是以1为首项,3为公比的等比数列,再求
是以1为首项,3为公比的等比数列,再求![]() .(2) (ⅰ)证明
.(2) (ⅰ)证明![]() 即证数列
即证数列![]() 是等差数列. (ⅱ)先求得
是等差数列. (ⅱ)先求得![]() ,所以
,所以![]() 或
或![]() ,再求
,再求![]() ,再检验
,再检验![]() 即得数列
即得数列![]() 的通项公式.
的通项公式.
(1)当![]() ,
,![]() ,
,![]() 时,
时,![]() .①
.①
当![]() 时,
时,![]() ,所以
,所以![]() .
.
当![]() 时,
时,![]() .②
.②
①-②得:![]() .因为
.因为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
所以![]() 是以1为首项,3为公比的等比数列,
是以1为首项,3为公比的等比数列,
所以![]() .
.
(2)(ⅰ)当![]() ,
,![]() ,
,![]() 时,
时,![]() .③
.③
当![]() 时,
时,![]() .④
.④
③-④得:![]() ,⑤
,⑤
所以![]() .⑥
.⑥
⑤-⑥得:![]() .
.
因为![]() ,所以
,所以![]() 即
即![]() ,
,
所以![]() 是等差数列.
是等差数列.
(ⅱ)因为![]() ,所以
,所以![]() .
.
因为![]() ,所以
,所以![]() ,所以
,所以![]() .
.
因为![]() ,所以
,所以![]() .又因为
.又因为![]() ,
,
所以![]() ,所以
,所以![]() 或
或![]() .
.
当![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,
所以![]() 不符合题意.
不符合题意.
当![]() 时,
时,![]() ,
,![]() ,
,
所以![]() 满足题意.
满足题意.
所以![]() .
.

练习册系列答案
相关题目