题目内容
已知函数
。
（1）求
的定义域及最小正周期；
（2）求的单调递减区间。
解】（1）由sinx≠0得x≠kπ(k∈Z)，
故f(x)的定义域为{x∈R|x≠kπ，k∈Z}．
因为f(x)＝
＝2cosx(sinx－cosx)
＝sin2x－cos2x－1
＝
sin
－1，
所以f(x)的最小正周期T＝
＝π.
（2）函数y＝sinx的单调递减区间为
(k∈Z)．
由2kπ＋
≤2x－
≤2kπ＋
，x≠kπ(k∈Z)．
得kπ＋
≤x≤kπ＋
(k∈Z)．
所以f(x)的单调递减区间为
(k∈Z)．
练习册系列答案
相关题目
．
的定义域
；
，求实数
的值．
．
在（0，+∞）上是减函数．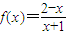
；
成立，若存在求出x；若不存在，请说明理由．
令
的定义域；
的奇偶性，并予以证明；
，猜想
之间的关系并证明.
，
的定义域；（2）证明：
，求
的取值范围。