Question

如果抛物线y=ax²－1上总有关于直线x+y=0对称的相异两点，试求a的范围.

Answer 1

解法一:设抛物线y=ax²－1上关于x+y=0对称的相异两点坐标为A(x₀,y₀)、B(－y₀,－x₀).

∵两点都在抛物线上，

∴ 

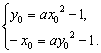
①－②，得y₀+x₀=a(x₀²－y₀²).

∵x₀+y₀≠0,∴x₀=.                                                                   ③

③代入②，得a²y₀²+ay₀+1－a=0.

∵y₀∈R,且(x₀,y₀),(－y₀,－x₀)相异，

∴Δ=a²－4a²(1－a)＞0.

∴a＞.∴a的取值范围是(，+∞).

解法二:设抛物线上关于直线x+y=0对称的两点所在直线方程为y=x+b,代入y=ax²－1,得ax²－x－b－1=0.

∵x∈R,且两点为相异两点，

∴Δ=1+4a(b+1)＞0,

即4ab+4a+1＞0.                                                                                ①

设两对称点为A(x₁,y₁)、B(x₂,y₂)，则

x₁+x₂=,y₁+y₂=+2b.

又∵+=0,

∴++b=0,即b=－.                                                                      ②

②代入①，得a＞.

∴a的取值范围是(，+∞).