题目内容
关于函数![]() ,有下列命题:
,有下列命题:
(1)![]() 为偶函数,
为偶函数,
(2)要得到函数g(x)=﹣4sin2x的图象,只需将f(x)的图象向右平移![]() 个单位,
个单位,
(3)y=f(x)的图象关于直线![]() 对称.
对称.
(4)y=f(x)在[0,2π]内的增区间为![]() 和
和![]() .
.
其中正确命题的序号为 (4) .
考点:
函数y=Asin(ωx+φ)的图象变换;正弦函数的奇偶性;正弦函数的单调性;正弦函数的对称性.
分析:
根据函数的奇偶性判断(1)的正误;根据余弦平移确定(2)的正误;根据函数的对称性确定(3)的正误;根据单调区间判断(4)的正误,即可得到结果.
解答:
解:(1)因为函数![]() ,所以
,所以![]() =4sin(2x+
=4sin(2x+![]() )不是偶函数;
)不是偶函数;
(2)将f(x)的图象向右平移![]() 个单位,得到y=4sin(2x+
个单位,得到y=4sin(2x+![]() ),不是函数g(x)=﹣4sin2x的图象,不正确;
),不是函数g(x)=﹣4sin2x的图象,不正确;
(3)![]() 时,
时,![]() 所以不关于直线
所以不关于直线![]() 对称.
对称.
(4)y=f(x)=![]() ,在[0,2π]内的增区间为
,在[0,2π]内的增区间为![]() 和
和![]() .正确.
.正确.
故答案为:(4)
点评:
本题考查函数y=Asin(ωx+φ)的图象变换,正弦函数的奇偶性,正弦函数的单调性,正弦函数的对称性,考查计算能力,推理能力,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,有下列命题:①f(x)的最大值为
,有下列命题:①f(x)的最大值为 ;②f(x)是以π为最小正周期的周期函数;③f(x)在区间(
;②f(x)是以π为最小正周期的周期函数;③f(x)在区间( ,
, )上单调递减;④将函数y=
)上单调递减;④将函数y= cos2x的图象向左平移
cos2x的图象向左平移 个单位后,将与f(x)的图象重合,其中正确命题的序号是 .
个单位后,将与f(x)的图象重合,其中正确命题的序号是 . ,有下列命题
,有下列命题 ;
;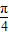 个单位而得到;
个单位而得到; ;
; 为单调递增函数;
为单调递增函数; ,有下列命题:
,有下列命题: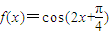 ;
; 图象的一条对称轴;
图象的一条对称轴;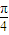 个单位得到;
个单位得到; ,有下列命题:
,有下列命题: 轴对称;
②当
轴对称;
②当 时,
时, 是增函数;当
是增函数;当 时,
时, ; ④当
; ④当 和
和 时,
时, ,有下列命题:
,有下列命题: 的表达式可以变换成
的表达式可以变换成
 ;
;
 为最小正周期的周期函数;
为最小正周期的周期函数; 对称;
④
对称;
④ 对称.
对称.