题目内容
某动点在平面直角坐标系第一象限的整点上运动(含第一象限x,y轴上的整点),其运动规律为(m,n)→(m+1,n+1)或(m,n)→(m+1,n-1).若该动点从原点出发,经过6步运动到(6,2)点,则有
9
9
种不同的运动轨迹.分析:根据题意知,该动点从原点出发,第一次运动到K(1,1),第二次从K点运动到I(2,2)或J(2,0),依此类推,最后到达A(6,2),画出图形如图所示.再数一数不同的运动轨迹,一共有9种不同的运动轨迹.即可得出答案.
解答: 解:根据题意知,该动点从原点出发,第一次运动到K(1,1),第二次从K点运动到I(2,2)或J(2,0),依此类推,最后到达A(6,2),如图所示.
解:根据题意知,该动点从原点出发,第一次运动到K(1,1),第二次从K点运动到I(2,2)或J(2,0),依此类推,最后到达A(6,2),如图所示.
则不同的运动轨迹有:
O→K→I→G→D→B→A;
或O→K→J→H→E→B→A;…
一共有9种不同的运动轨迹.
故答案为:9.
 解:根据题意知,该动点从原点出发,第一次运动到K(1,1),第二次从K点运动到I(2,2)或J(2,0),依此类推,最后到达A(6,2),如图所示.
解:根据题意知,该动点从原点出发,第一次运动到K(1,1),第二次从K点运动到I(2,2)或J(2,0),依此类推,最后到达A(6,2),如图所示.则不同的运动轨迹有:
O→K→I→G→D→B→A;
或O→K→J→H→E→B→A;…
一共有9种不同的运动轨迹.
故答案为:9.
点评:本小题主要考查进行简单的合情推理、新定义的应用等基础知识,考查数形结合思想.属于中档题.

练习册系列答案
相关题目
 ,
, 做匀速直线运动,质点A沿着水平方向向右运动.若
做匀速直线运动,质点A沿着水平方向向右运动.若 ,且两个动点必在某个时刻相遇,则动点B的运动路线所对应的函数f(x)的表达式是
,且两个动点必在某个时刻相遇,则动点B的运动路线所对应的函数f(x)的表达式是



 ,向量
,向量 .
. 的特征值
的特征值 、
、 和特征向量
和特征向量 ;
; 的值.
的值. .以直角坐标系原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为
.以直角坐标系原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为 .
. ;w.w.w.k.s.5.u.c.o.m
;w.w.w.k.s.5.u.c.o.m  ,向量
,向量 .
. 的特征值
的特征值 、
、 和特征向量
和特征向量 ;
; 的值.
的值. .以直角坐标系原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为
.以直角坐标系原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为 .
. ;www.7caiedu.cn
;www.7caiedu.cn 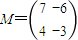 ,向量
,向量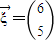 .
.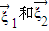 ;
;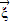 的值.
的值.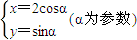 .以直角坐标系原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为
.以直角坐标系原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为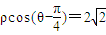 .
.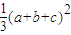 ;
;