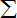题目内容

若f（m）=
n
i=0
mi
C
i
n
，则
log2f(3)
log2f(1)
=
3
3
．
分析：结合二项式定理可得f（m）=
n
i=0
mi
C
i
n
=（1+m）n，代入利用对数的运算性质可求
解答：解：∵f（m）=
n
i=0
mi
C
i
n
=（1+m）n
则
log2f(3)
log2f(1)
=
log2(1+m)3
log2(1+m)
=3
故答案为：3
点评：本题主要考查了二项展开式的通项的应用及对数的运算性质的应用，解题的关键是发现f（m）=
n
i=0
mi
C
i
n
=（1+m）n
练习册系列答案
相关题目
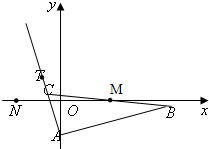精英家教网已知△ABC的边AB边所在直线的方程为x-3y-6=0，M（2，0）满足
BM
=
MC
，点T（-1，1）在AC边所在直线上且满足
AT
=
AB
．
（I）求AC边所在直线的方程；
（II）求△ABC外接圆的方程；
（III）若动圆P过点N（-2，0），且与△ABC的外接圆外切，求动圆P的圆心的轨迹方程．
请注意下面两题用到求和符号：
f（k）+f（k+1）+f（k+2）+…+f（n）=
n
i=k
f(i)，其中k，n为正整数且k≤n．
给出下列命题：
①“sinα＞sinβ”是“α＞β”的既不充分又不必要条件；
②若f（x）在某区间M上为增函数，则对于该区间上的任意x，总有f′（x）＞0；
③设空间任意一点O和不共线三点A、B、C，若点P满足向量关系
OP
=x
OA
+y
OB
+z
OC
，则P、A、B、C四点共面；
④若取值为x1，x2，x3…xn的频率分别为p1，p2，p3…pn，则其平均数为
n
i=1
xipi．
其中所有真命题的序号是
①④
①④
．
（2012•衡阳模拟）我们规定满足“f（-x）=-f（x）”的分段函数叫“对偶函数”．已知函数f（x）=
x2+4x，x≥0
g(x)，x＜0
是对偶函数．
（1）g（x）=
4x-x2
4x-x2
；
（2）若f[
n
i=1
1
i(i+1)
-
m
10
]＞0对任意的n∈N*都成立，则最大正整数m是
4
4
．
定义：若
h(x)
xk
在[k，+∞]上为增函数，则称h（x）为“k次比增函数”，其中k∈N*，已知f（x）=eax．
（Ⅰ）若f（x）是“1次比增函数”，求实数a的取值范围；
（Ⅱ）当a=
1
2
时，求函数g（x）=
f(x)
x
在[m，m+1]（m＞0）上的最小值；
（Ⅲ）求证：
n
i=1
1
i•(
e
)i
＜
7
2e
．
给出下列命题：
①“sinα＞sinβ”是“α＞β”的既不充分又不必要条件；
②若f（x）在某区间M上为增函数，则对于该区间上的任意x，总有f′（x）＞0；
③设空间任意一点O和不共线三点A、B、C，若点P满足向量关系
OP
=x
OA
+y
OB
+z
OC
，则P、A、B、C四点共面；
④若取值为x1，x2，x3…xn的频率分别为p1，p2，p3…pn，则其平均数为
n


i=1
xipi．
其中所有真命题的序号是______．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网