题目内容
已知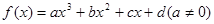 的对称中心为
的对称中心为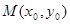 ,记函数
,记函数 的导函数为
的导函数为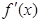 ,
,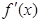 的导函数为
的导函数为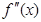 ,则有
,则有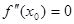 .若函数
.若函数 =
=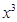 –
–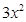 ,则可求得
,则可求得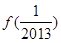 +
+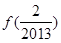 +
+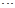
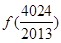 +
+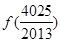 =( )
=( )
| A.–4025 | B.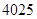 | C.–8050 | D.8050 |
C
解析试题分析:因为 时,
时,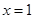 ,所以函数
,所以函数 的对称中心是
的对称中心是 ,则有
,则有 ,又
,又 ,所以
,所以 ,所以
,所以 .
.
考点:函数的对称性

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若函数 ,则下列结论正确的是 ( )
,则下列结论正确的是 ( )
A. , , 在 在 上是增函数 上是增函数 |
B. , , 在 在 上是减函数 上是减函数 |
C. , , 是偶函数 是偶函数 |
D. , , 是奇函数 是奇函数 |
下列函数中与 为同一函数的是
为同一函数的是
A. | B. | C. | D.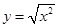 |
设偶函数 在
在 上为增函数,且
上为增函数,且 ,则不等式
,则不等式 的解集为( )
的解集为( )
A. | B. |
C. | D. |
 是定义在R上的奇函数且单调递减,若
是定义在R上的奇函数且单调递减,若 ,则
,则 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
对于函数 与
与 和区间D,如果存在
和区间D,如果存在 ,使
,使 ,则称
,则称 是函数
是函数 与
与 在区间D上的“友好点”.现给出两个函数:
在区间D上的“友好点”.现给出两个函数:
① ,
, ;②
;② ,
, ;③
;③ ,
, ;④
;④
 ,
, ,则在区间
,则在区间 上的存在唯一“友好点”的是( )
上的存在唯一“友好点”的是( )
| A.①② | B.③④ | C.②③ | D.①④ |
设函数 ,[x]表示不超过x的最大整数,则函数
,[x]表示不超过x的最大整数,则函数 的值域是( )
的值域是( )
| A.{0,1} | B.{0,-1} | C.{-1,1} | D.{1,1} |
函数 的图像关于 ( )
的图像关于 ( )
A. 轴对称 轴对称 | B.直线 | C.坐标原点对称 | D.直线 |
设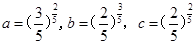 ,则
,则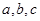 的大小关系是 ( )
的大小关系是 ( )
A.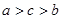 | B.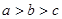 | C.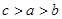 | D.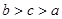 |