题目内容
对于函数 与
与 和区间D,如果存在
和区间D,如果存在 ,使
,使 ,则称
,则称 是函数
是函数 与
与 在区间D上的“友好点”.现给出两个函数:
在区间D上的“友好点”.现给出两个函数:
① ,
, ;②
;② ,
, ;③
;③ ,
, ;④
;④
 ,
, ,则在区间
,则在区间 上的存在唯一“友好点”的是( )
上的存在唯一“友好点”的是( )
| A.①② | B.③④ | C.②③ | D.①④ |
D.
解析试题分析:对于①,由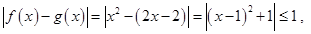 得
得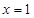 ,即为唯一的“友好点”;对于②,
,即为唯一的“友好点”;对于②,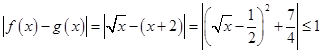 无解,故不存在“友好点”;对于③,
无解,故不存在“友好点”;对于③,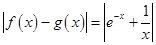 ,而
,而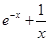 是
是 上的减函数,且
上的减函数,且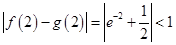 ,故
,故 与
与 在区间
在区间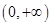 上有无穷多个“友好点”;对于④,
上有无穷多个“友好点”;对于④,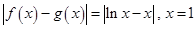 时,
时,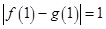 .令
.令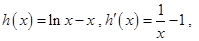 当
当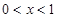 时,
时,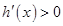 ;当
;当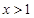 时,
时,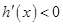 .
.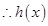 在
在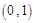 上是增函数,在
上是增函数,在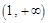 上是减函数,
上是减函数,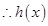 在
在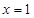 处取最大值,且
处取最大值,且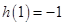 ,从而在
,从而在 上,
上, 恒成立,
恒成立,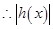 在
在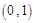 上是减函数,在
上是减函数,在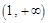 上是增函数,
上是增函数,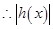 在
在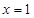 处取最小值,且
处取最小值,且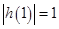 ,即
,即 与
与 有唯一的“友好点”.综上所述选D.
有唯一的“友好点”.综上所述选D.
考点:1.新定义“友好点”;2.函数的单调性、最值.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
已知定义在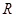 上的偶函数
上的偶函数 满足
满足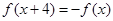 ,且在区间
,且在区间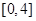 上是减函数则( )
上是减函数则( )
A. | B.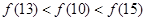 |
C. | D. |
函数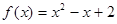 ,则下列关系中一定正确的是
,则下列关系中一定正确的是
A.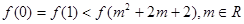 |
B.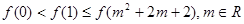 |
C.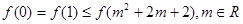 |
D.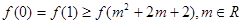 |
已知函数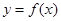 ,则该函数与直线
,则该函数与直线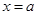 的交点个数有( )
的交点个数有( )
| A.1个 | B.2个 | C.无数个 | D.至多一个 |
已知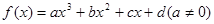 的对称中心为
的对称中心为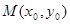 ,记函数
,记函数 的导函数为
的导函数为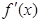 ,
,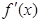 的导函数为
的导函数为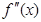 ,则有
,则有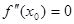 .若函数
.若函数 =
=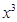 –
–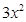 ,则可求得
,则可求得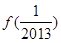 +
+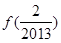 +
+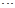
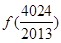 +
+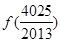 =( )
=( )
| A.–4025 | B.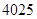 | C.–8050 | D.8050 |
函数 的图象( )
的图象( )
| A.关于原点对称 | B.关于直线 对称 对称 |
C.关于 轴对称 轴对称 | D.关于 轴对称 轴对称 |
已知函数f(x)= , 对任意m∈[-3,3],不等式f(mx-1)+f(2x)<0恒成立,则实数x的取值范围为( )
, 对任意m∈[-3,3],不等式f(mx-1)+f(2x)<0恒成立,则实数x的取值范围为( )
A.(-1, ) ) | B.(-2, ) ) | C.(-2, ) ) | D.(-2, ) ) |
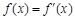 的实数根
的实数根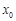 叫做函数的“新驻点”,若函数
叫做函数的“新驻点”,若函数 ,
,
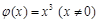 的“新驻点”分别为
的“新驻点”分别为 ,
,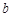 ,
,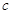 ,则
,则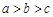


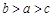
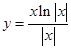 的图像可能是( )
的图像可能是( )