题目内容
20.函数f(θ)=$\overrightarrow{a}$•$\overrightarrow{b}$,向量$\overrightarrow{a}$=(sinθ,cosθ),$\overrightarrow{b}$=$(sinθ,\sqrt{3}sinθ+2cosθ)$,其中角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π.(1)若点P的坐标为$(\frac{1}{2}\;,\;\frac{{\sqrt{3}}}{2})$,求f(θ)的值;
(2)若点P(x,y)满足y=1,|x|≤1,试确定θ的取值范围,并求函数f(θ)的最小值.
分析 (1)利用平面向量的数量积的定义和坐标公式,建立条件关系,根据三角函数的定义,即可得到结论;
(2)作出不等式组对应的平面区域,利用数形结合即可得到f(θ)的最小值.
解答 解:(1)由P$(\frac{1}{2}\;,\;\frac{{\sqrt{3}}}{2})$,且0≤θ≤π得θ=$\frac{π}{3}$;
f(θ)=$\overrightarrow{a}$•$\overrightarrow{b}$=$si{n}^{2}θ+\sqrt{3}sinθcosθ+2co{s}^{2}θ$=$1+co{s}^{2}θ+\frac{\sqrt{3}}{2}sin2θ$
=$1+\frac{1+cos2θ}{2}+\frac{\sqrt{3}}{2}sin2θ$=$\frac{\sqrt{3}}{2}sin2θ+\frac{1}{2}cos2θ+\frac{3}{2}$=$sin(2θ+\frac{π}{6})+\frac{3}{2}$.
∴f(θ)=f($\frac{π}{3}$)=$sin(2×\frac{π}{3}+\frac{π}{6})+\frac{3}{2}$=2;
(2)如图,作出平面区域Ω为线段AB.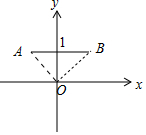
则得θ∈[$\frac{π}{4},\frac{3π}{4}$],
f(θ)=sin(2θ+$\frac{π}{6}$)+$\frac{3}{2}$,
∵θ∈[$\frac{π}{4}$,$\frac{3π}{4}$],
∴2θ+$\frac{π}{6}$∈[$\frac{2}{3}π$,$\frac{5}{3}π$],
∴f(θ)的最小值=f($\frac{2π}{3}$)=$\frac{3}{2}-1=\frac{1}{2}$.
点评 本题主要三角函数的图象和性质,利用平面向量的数量积公式进行化简是解决本题的根据,注意线性规划的应用,是中档题.

| A. | -2$\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 0 | D. | 1-$\sqrt{3}$ |
| A. | $\frac{x^2}{25}-\frac{y^2}{16}=1$ | B. | $\frac{x^2}{25}+\frac{y^2}{16}=1$ | ||
| C. | $\frac{x^2}{25}-\frac{y^2}{16}=1({x≠±5})$ | D. | $\frac{x^2}{25}+\frac{y^2}{16}=1({x≠±5})$ |
| A. | $\sqrt{2}f(-\frac{π}{3})<f(\frac{π}{4})$ | B. | $\sqrt{2}f(-\frac{π}{3})<f(-\frac{π}{4})$ | C. | $f(0)>\sqrt{2}f(-\frac{π}{4})$ | D. | $f(\frac{π}{6})<\sqrt{3}f(\frac{π}{3})$ |
 如图,已知△ABC中,D为边BC上靠近B点的三等分点,连接AD,E为线段AD的中点,若$\overrightarrow{CE}=m\overrightarrow{AB}+n\overrightarrow{AC}$,则m+n=$-\frac{1}{2}$.
如图,已知△ABC中,D为边BC上靠近B点的三等分点,连接AD,E为线段AD的中点,若$\overrightarrow{CE}=m\overrightarrow{AB}+n\overrightarrow{AC}$,则m+n=$-\frac{1}{2}$.
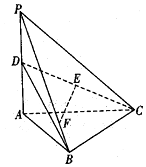 如图,三棱锥P-ABC中,PA⊥平面ABC,∠ABC=90°,PA=AC=2,D是PA的中点,E是CD的中点,点F在PB上,$\overrightarrow{PF}=3\overrightarrow{FB}$.
如图,三棱锥P-ABC中,PA⊥平面ABC,∠ABC=90°,PA=AC=2,D是PA的中点,E是CD的中点,点F在PB上,$\overrightarrow{PF}=3\overrightarrow{FB}$.