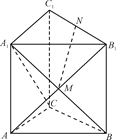
题目内容
如图,在三棱柱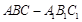 中,侧面
中,侧面 为菱形,且
为菱形,且 ,
, ,
, 是
是 的中点.
的中点.
(1)求证:平面 平面
平面 ;
;
(2)求证: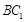 ∥平面
∥平面 .
.
(1)证明见解析;(2)见解析.
解析试题分析:(1)要证面面垂直,根据判定定理,要证线面垂直,也即要找线线垂直,在这个三棱柱中,已知的或者显而易见的垂直是我们首先要考虑的,如 是底面等腰三角形
是底面等腰三角形 的底边
的底边 的中点,则有
的中点,则有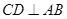 ,又侧面
,又侧面 是菱形且
是菱形且 ,那么在
,那么在 中可求得
中可求得 ,即
,即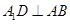 ,从而我们可得到
,从而我们可得到 ,结论得出;(2)要证线面平行,就是要在平面内找一条与待证直线平行的直线,这里我们可以想象一下,把直线
,结论得出;(2)要证线面平行,就是要在平面内找一条与待证直线平行的直线,这里我们可以想象一下,把直线 平移,平移到过平面
平移,平移到过平面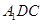 时,那么要找的直线就出来了,本题中把直线
时,那么要找的直线就出来了,本题中把直线 沿
沿 方向平移,当
方向平移,当 与
与 重合时,要找的直线就有了,因此我们通过连接
重合时,要找的直线就有了,因此我们通过连接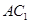 与
与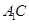 相交于
相交于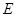 ,
,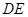 就是我们所需要的平行线.当然解题时注意定理所需的条件一个都不能少.
就是我们所需要的平行线.当然解题时注意定理所需的条件一个都不能少.
试题解析:(1)证明:∵ 为菱形,且
为菱形,且 ,
,
∴△ 为正三角形. 2分
为正三角形. 2分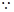
 是
是 的中点,∴
的中点,∴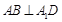 .
.
∵ ,
, 是
是 的中点,∴
的中点,∴ . 4分
. 4分
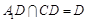 ,∴
,∴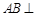 平面
平面 . 6分
. 6分
∵ 平面
平面 ,∴平面
,∴平面 平面
平面 . 8分
. 8分
(2)证明:连结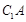 ,设
,设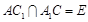 ,连结
,连结 .
.
∵三棱柱的侧面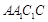 是平行四边形,∴
是平行四边形,∴ 为
为 中点. 10分
中点. 10分
在△ 中,又∵
中,又∵ 是
是 的中点,∴
的中点,∴ ∥
∥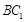 . 12分
. 12分
∵ 平面
平面 ,
, 平面
平面 ,∴
,∴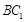 ∥平面
∥平面 . 14分
. 14分
考点:(1)面面垂直;(2)线面平行.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 中,底面
中,底面 是平行四边形,
是平行四边形, ,
, 平面
平面 ,
, ,
, 是
是 的中点.
的中点.
 平面
平面 ;
;  为坐标原点,射线
为坐标原点,射线 、
、 、
、 分别是
分别是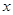 轴、
轴、 轴、
轴、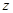 轴的正半轴,建立空间直角坐标系,已经计算得
轴的正半轴,建立空间直角坐标系,已经计算得 是平面
是平面 的法向量,求平面
的法向量,求平面 与平面
与平面
 ?,若存在,求出AM的长,若不存在,说明理由
?,若存在,求出AM的长,若不存在,说明理由 中,
中, 平面
平面 ,底面
,底面 .
.
 平面
平面 ;
; 平面
平面 ;
; 是
是 的中点,求三棱锥
的中点,求三棱锥 的体积.
的体积. 关于直线
关于直线 对称,
对称,
 .把
.把 沿
沿 折起(如图二),使二面角
折起(如图二),使二面角 的余弦值等于
的余弦值等于 .对于图二,完成以下各小题:
.对于图二,完成以下各小题:
 两点间的距离;
两点间的距离; 平面
平面 ;
; 所成角的正弦值.
所成角的正弦值. 中,底面
中,底面 是矩形,
是矩形, ,
, ,
,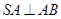 ,
, 是棱
是棱 的中点.
的中点.
 平面
平面 ;
;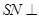 平面
平面 上是否存在一点
上是否存在一点 ,使得平面
,使得平面 平面
平面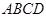 ?若存在,求出
?若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由. 上,B1E=3EC1,AC=BC=CC1=4.
上,B1E=3EC1,AC=BC=CC1=4.