��Ŀ����
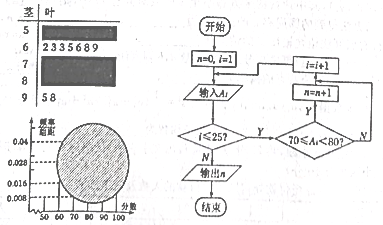
����Ŀ��ij��ͧ���쳧�з���һ������ͧ������ǰ5���µIJ������£�

��1����![]() ����
����![]() �Ļع�ֱ�߷���Ϊ
�Ļع�ֱ�߷���Ϊ![]() �ָ��ݱ��������Ѿ���ȷ�������
�ָ��ݱ��������Ѿ���ȷ�������![]() ��ֵΪ
��ֵΪ![]() ������
������![]() ��ֵ�������Ƹó�
��ֵ�������Ƹó�![]() �·ݵIJ���������������ȷ��
�·ݵIJ���������������ȷ��![]() ��
��
�����ʼ첿�ŷ��ָó�![]() �·���������ͧ�������������⣬Ҫ���ٻأ�����һ���ι�˾����ó������˽���ǰ��������������ͧ
�·���������ͧ�������������⣬Ҫ���ٻأ�����һ���ι�˾����ó������˽���ǰ��������������ͧ![]() �ң�������ι�˾����ͧ���ٻصĸ���.
�ң�������ι�˾����ͧ���ٻصĸ���.
���𰸡�(��)�𰸼�������(��)![]() .
.
��������������(��)���ݱ������![]() ��ƽ��ֵ������ع鷽�̼������
��ƽ��ֵ������ع鷽�̼������![]() ��ֵ������������ó�
��ֵ������������ó�![]() �·ݵIJ�����(��)������������һ�����·���ͧ��ţ�Ȼ���оٳ����ܵĽ�������ҳ�����Ҫ�����ϣ���������¼��ĸ���.
�·ݵIJ�����(��)������������һ�����·���ͧ��ţ�Ȼ���оٳ����ܵĽ�������ҳ�����Ҫ�����ϣ���������¼��ĸ���.
��⣺(1��![]()
��Ϊ�ع�ֱ��![]() ����
����![]() ����
����![]()
����![]() ��
��![]() ʱ��
ʱ��![]()
���Թ��Ƹó�![]() �·ݵIJ���Ϊ
�·ݵIJ���Ϊ![]() ��.
��.
����һ ��һ�·�������![]() ����ͧΪ
����ͧΪ![]() �����·�������
�����·�������![]() ����ͧΪ
����ͧΪ![]()
���ι�˾��ó�������һ�����·�������������ͧ�����п��ܽ����![]()
![]()
![]()
![]()
![]()
![]() �����֣�
�����֣�
����![]() ����ͧȫΪ���·������Ľ����
����ͧȫΪ���·������Ľ����![]() ��3�֣�
��3�֣�
����������ͧȫ��Ϊ���·������ĸ���Ϊ![]()
����������ͧ������һ��Ϊһ�·������ĸ���Ϊ![]() ��
��
�������ι�˾����ͧ���ٻصĸ���Ϊ��![]() .
.
���� ��һ�·�������![]() ����ͧΪ
����ͧΪ![]() ���·�������
���·�������![]() ����ͧΪ
����ͧΪ![]()
���ι�˾��ó�������һ�����·�������������ͧ�����п��ܽ����![]()
![]() ��10�֣����У�������ͧ������һ��Ϊһ�·������Ľ����
��10�֣����У�������ͧ������һ��Ϊһ�·������Ľ����![]() ��7�֣�
��7�֣�
����������ͧ������һ��Ϊһ�·������ĸ���Ϊ![]() ��
��
�������ι�˾����ͧ���ٻصĸ���Ϊ![]() .
.

 �Ƹ������������ϵ�д�
�Ƹ������������ϵ�д�