题目内容
抛物线C：y=ax2的准线为y=
，PM，PN切抛物线于M，N且与X轴交于A，B，|AB|=1．
（1）求a的值；
（2）求P点的轨迹．
解：（1）由已知：抛物线的准线为y=，
∴
，∴p=1…（2分）
∴抛物线为x2=2y即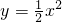
，
∴
…（5分）
（2）设
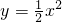∵，∴y′=x，∴kPM=x1
直线PM：
，即
令y=0得
即
同理PN：
，
…（9分）
由
得
∵|AB|=1，∴
，∴
∴（2x）2-8y=4即
…（12分）
∴P的轨迹方程为，轨迹是一条抛物线 …（13分）
分析：（1）根据抛物线的准线方程确定抛物线方程，即可求得a的值；
（2）先求出切线方程，得出A，B的坐标，利用|AB|=1，可得轨迹方程，从而可得P点的轨迹．
点评：本题考查抛物线方程，考查抛物线的切线方程，考查学生的计算能力，属于中档题．
，∴
，∴p=1…（2分）∴抛物线为x2=2y即
，∴
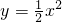…（5分）（2）设
∵
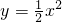，∴y′=x，∴kPM=x1直线PM：
，即令y=0得
即同理PN：
，…（9分）由
得∵|AB|=1，∴
，∴∴（2x）2-8y=4即
…（12分）∴P的轨迹方程为
，轨迹是一条抛物线 …（13分）分析：（1）根据抛物线的准线方程确定抛物线方程，即可求得a的值；
（2）先求出切线方程，得出A，B的坐标，利用|AB|=1，可得轨迹方程，从而可得P点的轨迹．
点评：本题考查抛物线方程，考查抛物线的切线方程，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
已知抛物线C：y=ax2（a＞0）上的点P（b，1）到焦点的距离为