题目内容
(2012•道里区三模)已知抛物线C:y=ax2(a>0)的焦点到准线的距离为
,且C上的两点A(x1,y1),B(x2,y2)关于直线y=x+m对称,并且x1x2=-
,那么m=( )
| 1 |
| 4 |
| 1 |
| 2 |
分析:先确定抛物线方程,设出直线AB方程代入抛物线方程,求出AB中点坐标,即可求得m的值.
解答:解:抛物线C:y=ax2(a>0)可化为x2=
y(a>0)
∵抛物线C:y=ax2(a>0)的焦点到准线的距离为
,
∴
=
,∴a=2
∴y=2x2,
∵C上的两点A(x1,y1),B(x2,y2)关于直线y=x+m对称,
∴直线AB斜率为-1,
设直线方程为y=-x+b与y=2x2联立得2x2+x-b=0
∴x1x2=-
=-
,∴b=1
∵x1+x2=-
,y1+y2=
,
∴AB中点坐标为(-
,
)
代入y=x+m得m=
故选A.
| 1 |
| a |
∵抛物线C:y=ax2(a>0)的焦点到准线的距离为
| 1 |
| 4 |
∴
| 1 |
| 2a |
| 1 |
| 4 |
∴y=2x2,
∵C上的两点A(x1,y1),B(x2,y2)关于直线y=x+m对称,
∴直线AB斜率为-1,
设直线方程为y=-x+b与y=2x2联立得2x2+x-b=0
∴x1x2=-
| b |
| 2 |
| 1 |
| 2 |
∵x1+x2=-
| 1 |
| 2 |
| 5 |
| 2 |
∴AB中点坐标为(-
| 1 |
| 4 |
| 5 |
| 4 |
代入y=x+m得m=
| 3 |
| 2 |
故选A.
点评:本题考查抛物线的标准方程,考查直线与抛物线的位置关系,考查韦达定理的运用,属于中档题.

练习册系列答案
 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
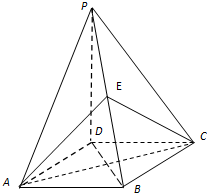 (2012•道里区三模)如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.
(2012•道里区三模)如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上. (2012•道里区三模)如图,设D是图中边长分别为1和2的矩形区域,E是D内位于函数y=
(2012•道里区三模)如图,设D是图中边长分别为1和2的矩形区域,E是D内位于函数y=