题目内容
若f (x) (x∈R)是以2为周期的偶函数,当x∈[0,1]时,f(x)=x
,则f(
),f(
),f(
)由小到大排列是
| 1 |
| 1000 |
| 98 |
| 19 |
| 101 |
| 17 |
| 104 |
| 15 |
f(
)<f(
)<f(
)
| 101 |
| 17 |
| 98 |
| 19 |
| 104 |
| 15 |
f(
)<f(
)<f(
)
.| 101 |
| 17 |
| 98 |
| 19 |
| 104 |
| 15 |
分析:因为当x∈[0,1]时,f(x)=x
,则函数f(x)在[0,1]上为增函数,再根据周期性和奇偶性把要比较的三个函数值都转化为[0,1]内的函数值即可.
| 1 |
| 1000 |
解答:解:因为函数的周期是2,所以6也是函数的周期,
所以f(
)=f(6-
)=f(
),
f(
)=f(6-
)=f(
),
f(
)=f(6+
)=f(
).
而f(x)是[0,1]上的增函数.由
<
<
,得f(
)<f(
)<f(
)
所以f(
)<f(
)<f(
).
故答案为f(
)<f(
)<f(
).
所以f(
| 98 |
| 19 |
| 16 |
| 19 |
| 16 |
| 19 |
f(
| 101 |
| 17 |
| 1 |
| 17 |
| 1 |
| 17 |
f(
| 104 |
| 15 |
| 14 |
| 15 |
| 14 |
| 15 |
而f(x)是[0,1]上的增函数.由
| 1 |
| 17 |
| 16 |
| 19 |
| 14 |
| 15 |
| 1 |
| 17 |
| 16 |
| 19 |
| 14 |
| 15 |
所以f(
| 101 |
| 17 |
| 98 |
| 19 |
| 104 |
| 15 |
故答案为f(
| 101 |
| 17 |
| 98 |
| 19 |
| 104 |
| 15 |
点评:本题是考查函数的单调性、奇偶性和周期性的综合题,考查数学转化思想,解答此题的关键是借助于函数的周期,把要比较的函数值转化到已知单调性的区间内.

练习册系列答案
相关题目
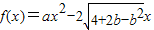 ,
,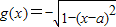 ,(a,b∈R)
,(a,b∈R)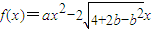 ,
,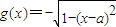 ,(a,b∈R)
,(a,b∈R)