题目内容
(本小题12分)
如图,已知四棱锥P—ABCD的底面是直角梯形,![]() ,AB=BC=2CD=2,PB=PC,
,AB=BC=2CD=2,PB=PC,
 侧面
侧面![]() 底面ABCD,O是BC的中点.
底面ABCD,O是BC的中点.
(Ⅰ)求证:![]() 平面ABCD;
平面ABCD;
(Ⅱ)求证:![]() ;
;
(Ⅲ)若二面角D—PA—O的余弦值为![]() ,求PB的长.
,求PB的长.
(本小题12分)
如图,已知四棱锥P—ABCD的底面是直角梯形,![]() ,AB=BC=2CD=2,PB=PC,
,AB=BC=2CD=2,PB=PC,
侧面![]() 底面ABCD,O是BC的中点.
底面ABCD,O是BC的中点.
 (Ⅰ)求证:
(Ⅰ)求证:![]() 平面ABCD;
平面ABCD;
(Ⅱ)求证:![]() ;
;
(Ⅲ)若二面角D—PA—O的余弦值为![]() ,求PB的长.
,求PB的长.
(Ⅰ)证明:因为![]() ,
,![]() 是
是![]() 的中点,
的中点,
所以![]()
![]() ,
,
 又侧面PBC⊥底面ABCD,
又侧面PBC⊥底面ABCD,![]() 平面
平面![]() ,
,
面PBC![]() 底面ABCD
底面ABCD![]() ,
,
所以![]() 平面
平面![]() .
.
(Ⅱ)证明:以点![]() 为坐标原点,建立如图空间直角坐标系
为坐标原点,建立如图空间直角坐标系![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,
,
![]() ,
,
因为![]() ,所以
,所以![]() ,
,
即![]() .
.
(Ⅲ)解:设平面![]() 和平面
和平面![]() 的法向量分别为
的法向量分别为![]() ,
,
注意到![]() ,
,![]() ,
,![]() ,
,
由 ,令
,令![]() 得,
得,![]() ,
,
由 令
令![]() 得,
得,![]() ,
,
所以 ,
,
解之得![]() ,所以
,所以![]() 为所求.
为所求.

练习册系列答案
相关题目
 是定义在
是定义在 上的偶函数,已知
上的偶函数,已知 时,
时, .
.
 的圆柱.
的圆柱.
 的方程
的方程
 .
.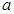 的取值范围.
的取值范围.