题目内容
如图,在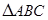 中,
中,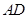 为
为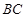 边上的中线,
边上的中线,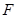 为
为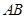 上任意一点,
上任意一点,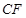 交
交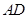 于点
于点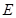 .求证:
.求证: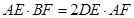 .
.
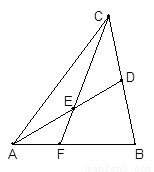
【解析】本试题主要是考查了平面几何中相似三角形性质的运用。根据已知条件,首先做辅助线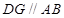 ,然后利用平行性得到相似比,
,然后利用平行性得到相似比,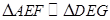 ,
,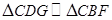 ,然后得到比例相等。充分利用比值问题转化得到结论。
,然后得到比例相等。充分利用比值问题转化得到结论。
证明:过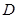 作
作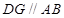 ,交
,交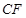 于
于 ,∴
,∴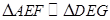 ,
,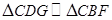 ,
,
∴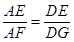 ,
,  , ∵
, ∵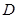 为
为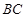 的中点,
的中点,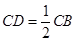 ,
,
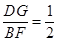 ,
,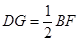 ,
,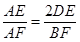 ,即
,即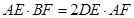 .
.
【答案】
见解析

练习册系列答案
相关题目
题目内容
如图,在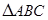 中,
中,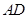 为
为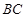 边上的中线,
边上的中线,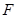 为
为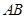 上任意一点,
上任意一点,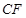 交
交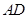 于点
于点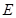 .求证:
.求证: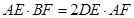 .
.
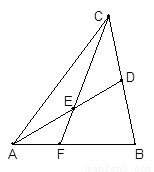
【解析】本试题主要是考查了平面几何中相似三角形性质的运用。根据已知条件,首先做辅助线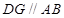 ,然后利用平行性得到相似比,
,然后利用平行性得到相似比,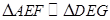 ,
,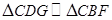 ,然后得到比例相等。充分利用比值问题转化得到结论。
,然后得到比例相等。充分利用比值问题转化得到结论。
证明:过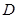 作
作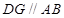 ,交
,交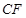 于
于 ,∴
,∴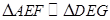 ,
,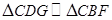 ,
,
∴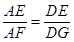 ,
,  , ∵
, ∵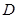 为
为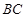 的中点,
的中点,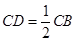 ,
,
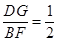 ,
,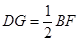 ,
,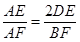 ,即
,即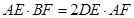 .
.
见解析
