题目内容
用反证法证明:已知 ,
, ,
, ,求证:
,求证: ,
, ,
, .
.
 ,
, ,
, ,求证:
,求证: ,
, ,
, .
.证明详见解析.
试题分析:根据应用反证法证明命题的一般步骤:先假设原命题的结论不成立,由此找出矛盾,从而肯定结论.本题先假设
 不都是正数,结合
不都是正数,结合 可知三个数中必有两个为负数,一个为正数,根据本题中的条件
可知三个数中必有两个为负数,一个为正数,根据本题中的条件 互相进行轮换后都没有变化,从而不妨设
互相进行轮换后都没有变化,从而不妨设 ,进而根据条件得出
,进而根据条件得出 ,由此推导出
,由此推导出 ,这与条件
,这与条件 矛盾,从而可肯定原结论正确.
矛盾,从而可肯定原结论正确.假设
 不都是正数 1分
不都是正数 1分由
 可知,这三个数中必有两个为负数,一个为正数 2分
可知,这三个数中必有两个为负数,一个为正数 2分不妨设

则由
 可得
可得 4分
4分又
 ,∴
,∴ 5分
5分 即
即 7分
7分∵
 ,∴
,∴
即
 9分
9分这与已知
 矛盾
矛盾所以假设不成立.因此
 成立 10分
成立 10分
练习册系列答案
相关题目
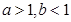 ,求证:
,求证: ;
; ,且
,且 ,
, .
. <a<c+
<a<c+ <
<
 ,那么
,那么 ”时,假设的内容应是 ( )
”时,假设的内容应是 ( )

 或
或 