Question

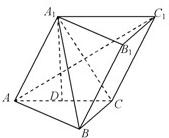已知三棱柱ABC-A₁B₁C₁，A₁在底面ABC上的射影恰为AC的中点D，∠BCA=90°，AC=BC=2，又知BA₁⊥AC₁
（1）求证：AC₁⊥平面A₁BC；
（2）求二面角A-A₁B-C的余弦值的大小．

Answer 1

分析：（1）根据题意可知BC⊥AC，而A₁D⊥底ABC，所以A₁D⊥BC，A₁D∩AC=D，从而BC⊥面A₁AC，则BC⊥AC₁，又因为BA₁⊥AC₁，BA₁∩BC=B，
满足线面垂直的判定定理，从而AC₁⊥底A₁BC；
（2）设AC₁∩A₁C=O，作OE⊥A₁B于E，连AE，由（1）所以A₁B⊥AE，根据二面角的平面角的定义可知∠AEO为二面角平面角，在Rt△A₁BC中求出OE，AO，AE，从而求出二面角余弦．

解答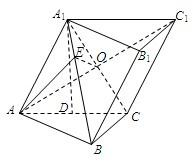：解：（1）证明：∠BCA=90°得BC⊥AC，因为A₁D⊥底ABC，
所以A₁D⊥BC，A₁D∩AC=D，所以BC⊥面A₁AC，
所以BC⊥AC₁（3分）
因为BA₁⊥AC₁，BA₁∩BC=B，
所以AC₁⊥底A₁BC（1分）
（2）设AC₁∩A₁C=O，作OE⊥A₁B于E，连AE，由（1）
所以A₁B⊥AE，所以∠AEO为二面角平面角，（2分）
在Rt△A₁BC中OE=

2

2

，AO=

3

，AE=

14

2

，
所以cosα=

7

7

，所以二面角余弦

7

7

点评：本题主要考查了直线与平面垂直的判定，以及二面角的度量等有关问题，同时考查了数形结合、化归与转化的数学思想方法，以及空间想象能力、推理论证能力和运算求解能力，属于中档题．