题目内容
如图，在半径为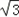
、圆心角为60°的扇形的弧上任取一点P，作扇形的内接矩形PNMQ，使点Q在OA上，点（N，M）在OB上，设矩形PNMQ的面积为y，
（1）按下列要求写出函数的关系式：
①设PN=x，将y表示成x的函数关系式；
②设∠POB=θ，将y表示成θ的函数关系式；
（2）请你选用（1）中的一个函数关系式，求出y的最大值．
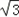、圆心角为60°的扇形的弧上任取一点P，作扇形的内接矩形PNMQ，使点Q在OA上，点（N，M）在OB上，设矩形PNMQ的面积为y，（1）按下列要求写出函数的关系式：
①设PN=x，将y表示成x的函数关系式；
②设∠POB=θ，将y表示成θ的函数关系式；
（2）请你选用（1）中的一个函数关系式，求出y的最大值．
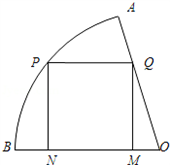
解：（1）①因为ON=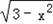
，OM=
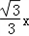，所以MN=
，
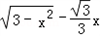所以y=x（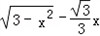
） x∈（0，
）．
②因为PN=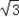
sinθ，ON=
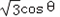，OM=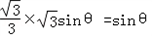
，
所以MN=ON﹣OM=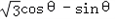
所以y=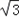
sinθ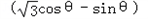
，
即y=3sinθcosθ﹣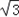
sin2θ，θ∈（0，
）
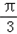（2）选择y=3sinΘcosΘ﹣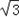
sin2θ=
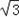sin（2θ+
）﹣
，
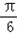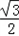∵Θ∈（0，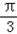
）∴
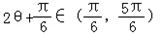
所以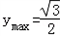
．
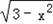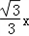，OM=，所以MN=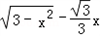，所以y=x（
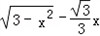） x∈（0，）．②因为PN=
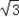sinθ，ON=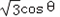，OM=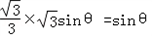，所以MN=ON﹣OM=
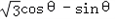
所以y=
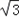sinθ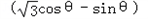，即y=3sinθcosθ﹣
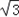sin2θ，θ∈（0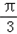，）（2）选择y=3sinΘcosΘ﹣
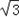sin2θ=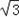sin（2θ+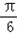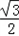）﹣，∵Θ∈（0，
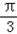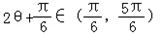
）∴所以
．
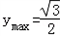练习册系列答案
冲刺100分1号卷系列答案
期末好成绩系列答案
相关题目
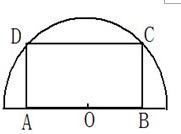如图，在半径为30cm的半圆形（O为圆心）铝皮上截取一块矩形材料ABCD，其中点A、B在直径上，点C、D在圆周上．
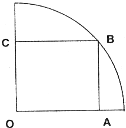如图，在半径为30cm的
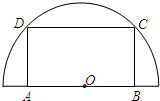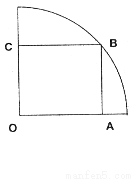
（2013•闵行区二模）如图，在半径为20cm的半圆形（O为圆心）铝皮上截取一块矩形材料ABCD，其中点A、B在直径上，点C、D在圆周上．
（2013•湖南）如图，在半径为
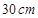的
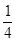圆形（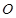
为圆心）铝皮上截取一块矩形材料
，其中点
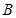在圆上，点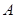
、
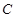在两半径上，现将此矩形铝皮
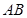为母线的圆柱形罐子的侧面（不计剪裁和拼接损耗），设矩形的边长
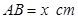，圆柱的体积为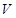
.
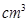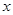的函数关系式，并指出定义域；