题目内容
已知函数 ,
,
(1)讨论函数的奇偶性;
(2)证明:f(x)>0.
解:(1)该函数为偶函数.
由2x-1≠0解得x≠0即义域为{x|x≠0}关于原点对称
f(-x)=( )(-x)=-(
)(-x)=-( +
+ )x
)x
=( )x=(
)x=( )x=(
)x=( )x=f(x)
)x=f(x)
故该函数为偶函数.
(2)证明:任取x∈{x|x≠0}
当x>0时,2x>20=1且x>0,
∴2x-1>0,
故
从而
当x<0时,-x>0,
∴f(-x)>0,
又因为函数为偶函数,
∴f(x)=f(-x)>0,
∴f(x)>0在定义域上恒成立.
分析:(1)由2x-1≠0解得义域为{x|x≠0},关于原点对称.f(-x)=( )(-x)=(
)(-x)=( )x=f(x),故该函数为偶函数.
)x=f(x),故该函数为偶函数.
(2)任取x∈{x|x≠0},当x>0时,2x>20=1且x>0,故 ,从而
,从而 .当x<0时,-x>0,故f(-x)>0,由函数为偶函数,能证明f(x)>0在定义域上恒成立.
.当x<0时,-x>0,故f(-x)>0,由函数为偶函数,能证明f(x)>0在定义域上恒成立.
点评:本题考查函数的奇偶性的判断和证明f(x)>0.解题时要认真审题,注意指数函数性质的灵活运用.
由2x-1≠0解得x≠0即义域为{x|x≠0}关于原点对称
f(-x)=(
 )(-x)=-(
)(-x)=-( +
+ )x
)x=(
 )x=(
)x=( )x=(
)x=( )x=f(x)
)x=f(x)故该函数为偶函数.
(2)证明:任取x∈{x|x≠0}
当x>0时,2x>20=1且x>0,
∴2x-1>0,
故

从而

当x<0时,-x>0,
∴f(-x)>0,
又因为函数为偶函数,
∴f(x)=f(-x)>0,
∴f(x)>0在定义域上恒成立.
分析:(1)由2x-1≠0解得义域为{x|x≠0},关于原点对称.f(-x)=(
 )(-x)=(
)(-x)=( )x=f(x),故该函数为偶函数.
)x=f(x),故该函数为偶函数. (2)任取x∈{x|x≠0},当x>0时,2x>20=1且x>0,故
 ,从而
,从而 .当x<0时,-x>0,故f(-x)>0,由函数为偶函数,能证明f(x)>0在定义域上恒成立.
.当x<0时,-x>0,故f(-x)>0,由函数为偶函数,能证明f(x)>0在定义域上恒成立.点评:本题考查函数的奇偶性的判断和证明f(x)>0.解题时要认真审题,注意指数函数性质的灵活运用.

练习册系列答案
相关题目
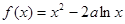 ,
,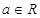
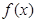 单调区间;
单调区间;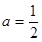 时,证明:当
时,证明:当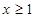 时,证明:
时,证明: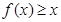 。
。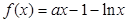
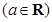 .
.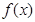 在定义域内的极值点的个数;
在定义域内的极值点的个数; 处取得极值,对
处取得极值,对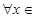
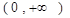 ,
,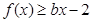 恒成立,求实数
恒成立,求实数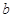 的取值范围.
的取值范围. 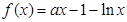
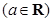 .
.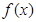 在定义域内的极值点的个数;
在定义域内的极值点的个数;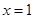 处取得极值,对
处取得极值,对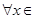
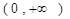 ,
,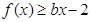 恒成立,求实数
恒成立,求实数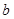 的取值范围;
的取值范围;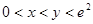 且
且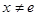 时,试比较
时,试比较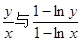 的大小.
的大小. .
. 函数
函数 的单调性;
的单调性; 为偶数时,正项数列
为偶数时,正项数列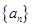 满足
满足 ,求
,求 时,求证:
时,求证: .
. 。(1)讨论函数
。(1)讨论函数 的单调性;(2)当
的单调性;(2)当 时,设
时,设 ,若
,若 时,
时, 恒成立。求整数
恒成立。求整数 的最大值。
的最大值。